Биполярный транзистор
В программе PSpice используется схема замещения биполярного транзистора в виде адаптированной модели Гуммеля–Пуна, которая по сравнению с исходной моделью позволяет учесть эффекты, возникающие при больших смещениях на переходах [4, 25, 33, 45, 47, 53]. Эта модель автоматически упрощается до более простой модели Эберса–Молла, если опустить некоторые параметры. Эквивалентные схемы этих моделей для n–p–n-структуры изображены на рис. 4.4. Параметры полной математической модели биполярного транзистора приведены в табл. 4.2.
Таблица 4.2
| Имя параметра | Параметр | Значение по умолчанию | Единица измерения | ||||
| IS | Ток насыщения при температуре 27 | 10 | А | ||||
| BF | Максимальный коэффициент усиления тока в нормальном режиме в схеме с ОЭ (без учета токов утечки) | 100 | |||||
| BR | Максимальный коэффициент усиления тока в инверсном режиме в схеме с ОЭ | 1 | |||||
| NF | Коэффициент неидеальности в нормальном режиме | 1 | |||||
| NR | Коэффициент неидеальности в инверсном режиме | 1 | |||||
| ISE (C2) * | Ток насыщения утечки перехода база–эмиттер | 0 | А | ||||
| ISC (C4) * | Ток насыщения утечки перехода база–коллектор | 0 | А | ||||
| IKF (IK) * | Ток начала спада зависимости BF от тока коллектора в нормальном режиме |  | А | ||||
| IKR* | Ток начала спада зависимости BR от тока эмиттера в инверсном режиме |  | А | ||||
| NE* | Коэффициент неидеальности перехода база–эмиттер | 1,5 | |||||
| NC* | Коэффициент неидеальности коллекторного перехода | 1,5 | |||||
| NK | Коэффициент, определяющий множитель Qb | 0,5 | |||||
| ISS | Обратный ток p–n-перехода подложки | 0 | A | ||||
| NS | Коэффициент неидеальности перехода подложки | 1 | |||||
| VAF (VA) * | Напряжение Эрли в нормальном режиме |  | В | ||||
| VAR (VB) * | Напряжение Эрли в инверсном режиме |  | В | ||||
| RC | Объемное сопротивление коллектора | 0 | Ом | ||||
| RE | Объемное сопротивление эмиттера | 0 | Ом | ||||
| RB | Объемное сопротивление базы (максимальное) при нулевом смещении перехода база–эмиттер | 0 | Ом | ||||
| RBM* | Минимальное сопротивление базы при больших токах | RB | Ом | ||||
| IRB* | Ток базы, при котором сопротивление базы уменьшается на 50% полного перепада между RB и RBM |  | А | ||||
| TF | Время переноса заряда через базу в нормальном режиме | 0 | с | ||||
| TR | Время переноса заряда через базу в инверсном режиме | 0 | с | ||||
| QCO | Множитель, определяющий заряд в эпитаксиальной области | 0 | Кл | ||||
| RCO | Сопротивление эпитаксиальной области | 0 | Ом | ||||
| VO | Напряжение, определяющее перегиб зависимости тока эпитаксиальной области | 10 | В | ||||
| GAMMA | Коэффициент легирования эпитаксиальной области | 10 | - | ||||
| XTF | Коэффициент, определяющий зависимость TF от смещения база–коллектор | 0 | |||||
| VTF | Напряжение, характеризующее зависимость TF от смещения база–коллектор |  | В | ||||
| ITF | Ток, характеризующий зависимость TF от тока коллектора при больших токах | 0 | А | ||||
| PTF | Дополнительный фазовый сдвиг на граничной частоте транзистора  | 0 | град. | ||||
| CJE | Емкость эмиттерного перехода при нулевом смещении | 0 | пФ | ||||
| VJE (PE) | Контактная разность потенциалов перехода база–эмиттер | 0,75 | В | ||||
| MJE (ME) | Коэффициент, учитывающий плавность эмиттерного перехода | 0,33 | |||||
| CJC | Емкость коллекторного перехода при нулевом смещении | 0 | Ф | ||||
| VJC (PC) | Контактная разность потенциалов перехода база–коллектор | 0,75 | В | ||||
| MJC (MC) | Коэффициент, учитывающий плавность коллекторного перехода | 0,33 | |||||
| CJS (CCS) | Емкость коллектор–подложка при нулевом смещении | 0 | Ф | ||||
| VJS (PS) | Контактная разность потенциалов перехода коллектор–подложка | 0,75 | В | ||||
| MJS (MS) | Коэффициент, учитывающий плавность перехода коллектор-подложка | 0 | - | ||||
| XCJC | Коэффициент расщепления емкости база–коллектор | 1 | |||||
| FC | Коэффициент нелинейности барьерных емкостей прямосмещенных переходов | 0,5 | |||||
| EG | Ширина запрещенной зоны | 1,11 | эВ | ||||
| XTB | Температурный коэффициент BF и BR | 0 | |||||
| XTI(PT) | Температурный коэффициент IS | 3 | |||||
| TRE1 | Линейный температурный коэффициент RE | 0 |  | ||||
| TRE2 | Квадратичный температурный коэффициент RE | 0 |  | ||||
| TRB1 | Линейный температурный коэффициент RB | 0 |  | ||||
| TRB2 | Квадратичный температурный коэффициент RB | 0 |  | ||||
| TRM1 | Линейный температурный коэффициент RBM | 0 |  | ||||
| TRM2 | Квадратичный температурный коэффициент RBM | 0 |  | ||||
| TRC1 | Линейный температурный коэффициент RC | 0 |  | ||||
| TRC2 | Квадратичный температурный коэффициент RC | 0 |  | ||||
| KF | Коэффициент, определяющий спектральную плотность фликкер–шума | 0 | |||||
| AF | Показатель степени, определяющий зависимость спектральной плотности фликкер–шума от тока через переход | 1 | |||||
| T_MEASURED | Температура измерений |  | |||||
| T_ABS | Абсолютная температура |  | |||||
| T_REL_GLOBAL | Относительная температура |  | |||||
| T_REL_LOCAL | Разность между температурой транзистора и модели-прототипа |  |
* Для модели Гуммеля–Пуна.
Примечания. 1. В круглых скобках в левой графе таблицы указаны альтернативные обозначения параметров. Параметр RB для модели Эберса–Молла имеет смысл объемного сопротивления базы, не зависящего от тока базы. Остальные параметры имеют одинаковый смысл для моделей Эберса–Молла и Гуммеля–Пуна.

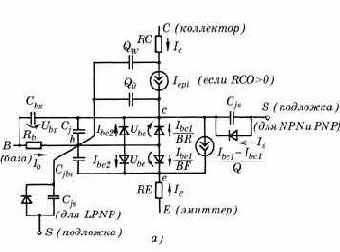 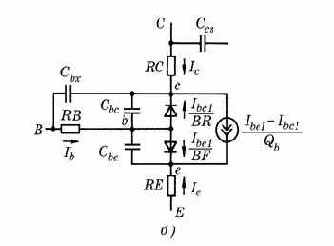 Рис. 4.4. Схема замещения биполярного n–p–n-транзистора: а - модель Гуммеля–Пуна; б - передаточная модель Эберса–Молла |
Статический режим транзистора. Режим описывается следующими соотношениями (см.рис. 4.4, а):
Ib = Ibe1/BF + Ibe2 + Ibc1/BR + Ibc2;
Ic = Ibe1/Qb–Ibc1/Qb–Ibc1/BR–Ibc2;
Ibe1 =IS[exp(Vbe/(NF·Vt)) – 1];
Ibe2 =ISE[exp(Vbe/(NE·Vt)) – 1];
Ibc1 =IS[exp(Vbc/(NR·Vt)) – 1];
Ibc2 =ISC[exp(Vbc/(NC·Vt) – 1];
Qb =Q1[1 + (1 + 4Q2)

Q1=1/(1-Vbc/VAF-Vbe/VAR), Q2=Ibe1/IKF+Ibc1/IKR;
Is =ISS [exp(Vjs/(NS·Vt)) – 1].
На рис 4.4 приняты обозначения: Ib
– ток базы; Ic – ток коллектора; Ibe1 – ток коллектора в нормальном режиме; Ibc1 – ток коллектора в инверсном режиме; Ibe2, Ibc2 – составляющие тока перехода база–эмиттер, вызванные неидеальностью перехода; Is
– ток подложки; Vbe, Vbc
–
напряжения на переходе внутренняя база–эмиттер и внутренняя база–коллектор; Vbs – напряжение внутренняя база–подложка; Vbn – напряжение внутренняя база–подложка для режима квазинасыщения; Vbx – напряжение база–внутренний коллектор; Vce – напряжение внутренний коллектор–внутренний эмиттер; Vjs – напряжение внутренний коллектор–подложка для NPN транзистора, напряжение внутренняя подложка–коллектор для PNP транзистора или напряжение внутренняя база–подложка для LPNP транзистора.
Объемное сопротивление базы Rb
характеризуется двумя составляющими. Первая составляющая RB определяет сопротивление вывода базы и сопротивление внешней области базы, которое не зависит от тока базы Ib. Вторая составляющая RBM характеризует сопротивление активной области базы, находящейся непосредственно под эмиттером; это сопротивление зависит от тока Ib. Объемное сопротивление базы Rb определяется следующими выражениями в зависимости от значения параметра IRB
Rb =

где

Замечание. В программе PSpice токи, втекающие в транзистор, считаются положительными. Поэтому в активном нормальном режиме в n–p–n-структуре (рис. 4.4) Ic>0, Ib>0, Ie<0. Для структуры p–n–p все напряжения и токи имеют противоположный знак.
Динамические свойства переходов. Они учтены включением в модель емкостей коллектора, эмиттера и подложки, которые имеют диффузионные и барьерные составляющие. Емкость перехода база–эмиттер равна сумме диффузионной (Ctbe) и барьерной (Cjbe) составляющих:
Cbe = Ctbe + Cjbe,
где Ctbe = tf·Gbe; Gbe = dIbe/dVbe – дифференциальная проводимость перехода база–эмиттер в рабочей точке по постоянному току;
tf =TF[1+XTF(3x
-2x )exp(Vbc/(1,44VTF))], x=Ibe1/(Ibe1+ITF);

Емкость перехода база-коллектор расщепляется на две составляющие:
емкость между внутренней базой и коллектором Cbc,
Cbc = Ctbc
+ XCJC·Cjbc,
где Cbct = TR·Gbc, Gbc=dIbc1/dVbc;

и емкость между внешним выводом базы и коллектором Cbx,

Емкость коллектор-подложка равна

Режим квазинасыщения. Этот режим характеризуется прямым смещением перехода внутренняя база–коллектор, в то время как переход наружная база–коллектор остается смещенным в обратном направлении. В расширенной модели Гуммеля–Пуна этот эффект моделируется с помощью дополнительного управляемого источника тока Iepi и двух нелинейных емкостей, заряды которых на рис. 4.4,а
обозначены Qo и Qw. Эти изменения вносятся в модель, если задан параметр RCO [59 ]:

где

Температурная зависимость. Эта зависимость параметров элементов эквивалентной схемы биполярного транзистора устанавливается с помощью следующих выражений:
IS(T)=IS·exp[EG(T)/Vt(T) (T/Tnom–1)] (T/Tnom)

ISE(T)=(ISE/ bf)·exp[EG(T)/(NE·Vt(T)) (T/Tnom–1)] (T/Tnom)

ISC(T)=(ISC/ bf)·exp[EG(T)/(NC·Vt(T)) (T/Tnom–1)] (T/Tnom)

ISS(T)=(ISS/bf) ·exp[EG(T)/(NS·Vt(T)) (T/Tnom–1)] (T/Tnom)

BF(T)=BF·bf, BR(T)=BR·bf, bf=(T/Tnom)

RE(T)=RE [1+TRE1(T–Tnom)+TRE2 (T–Tnom)

RB(T)=RB [1+TRB1(T–Tnom)+TRB2 (T–Tnom)

RBM(T)=RBM [1+TRM1(T–Tnom)+TRM2(T–Tnom)

RC(T)=RC[1+TRC1(T–Tnom)+TRC2 (T–Tnom)

VJE(T)=VJE·T/Tnom–3Vt ·ln(T/Tnom) –EG(Tnom) ·T/Tnom+EG(T);
VJC(T)=VJC·T/Tnom–3Vt ·ln(T/Tnom) –EG(Tnom) ·T/Tnom+EG(T);
VJS(T)=VJS·T/Tnom–3Vt ·ln(T/Tnom) –EG(Tnom)·T/Tnom+EG(T);
CJE(T)=CJE{1+MJE [0,0004(T–Tnom)+1–VJE(T)/VJE]};
CJC(T)=CJC{1+MJC [0,0004(T–Tnom)+1–VJC(T)/VJC]};
CJS(T)=CJS{1+MJS [0,0004(T–Tnom)+1–VJS(T)/VJS]};
KF(T)=KF·VJC(T)/VJC, AF(T)=AF·VJC(T)/VJC.
Зависимость EG от температуры описана в разд. 4.2.
Линейная схема замещения биполярного транзистора. Схема приведена на рис. 4.5. В нее дополнительно включены источники флюктуационных токов. Тепловые шумы IшRB, IшRC
и IшRE , создаваемые резисторами Rb, RC и RE, имеют спектральные плотности
S



Источники тока Iшb, Iшc, характеризующие дробовой и фликкер–шумы в цепях базы и коллектора, имеют соответственно спектральные плотности:
Sb = 2qIb
+ KF·Ib


Рис. 4.5. Линейная схема замещения биполярного транзистора с включением источников шума |
IS=IS·Area, ISE=ISE·Area, ISC=ICS·Area, ISS=ISS·Area, IKF=IKF·Area, IKR=IKR·Area, IRB=IRB·Area, ITF=ITF·Area, CJC=CJC·Area, CJE=CJE·Area, CJS=CJS·Area, RBB=RBB/Area, RE=RE/Area, RC=RC/Area, QCO=QCO·Area.
Значение Area указывается в задании на моделирование при включении транзистора в схему, по умолчанию Area=1.
В качестве примера приведем список параметров модели Гуммеля-Пуна биполярного транзистора КТ316Д
.model KT316D NPN(IS=2.75f XTI=3 EG=1.11 VAF=96 BF=136.5
+ NE=2.496 ISE=12.8pA IKF=97.23m XTB=1.5 VAR=55 BR=.66
+ NC=2 ISC=15.5p IKR=.12 RB=70.6 RC=8.4 CJC=4.1pF VJC=.65
+ MJC=.33 FC=.5 VJE=.69 CJE=1.16pF MJE=.33 TR=27.8n
+ TF=79.0p ITF=.151 VTF=25 XTF=2)