Постепенное расширение потока

Постепенное расширение трубы называется диффузором. Движение жидкости в диффузоре сопровождается уменьшением скорости и повышением давления. Частицы жидкости движутся вперёд, в сторону более высокого давления, по инерции за счёт своей кинетической энергии, которая уменьшается по направлению движения. Кроме того, за счёт расширения трубы частицы жидкости движутся не только вдоль оси потока, но и в направлении от оси к стенкам. В каком-то сечении инерция жидкости уменьшается до такой степени, что её не хватает для преодоления повышающегося давления. Тогда такие частицы жидкости останавливаются или даже начинают двигаться в обратном направлении. В результате возникают вихревые потоки и потоки, отрывающиеся от стенки. Эти явления зависят от скорости и интенсивности расширения потока. Кроме того, в диффузоре происходят обычные потери на трение, подобные потерям по длине в трубах постоянного сечения. Таким образом, потери энергии в диффузоре

складываются из потерь на трение по длине и потерь на вихреобразование за счёт расширения:

Для определения этих величин рассмотрим круглый диффузор с углом отклонения стенки от оси, равным

, и параметрами, приведёнными на рисунке. Определим потери на трение на произвольном элементарном участке диффузора длиной

. Увеличение радиуса диффузора на этом участке составит

. С учётом этого

Тогда потери энергии на этом элементарном участке по формуле Дарси составят

Из условия постоянства расхода можно записать

Отсюда, выразив

, получим:

где

- соответственно скорость жидкости и радиус диффузора

в начале произвольно выбранного участка диффузора

. Их можно рассматривать, как текущие значения параметров.

Подставив полученные выражения в формулу для

, получим:

После интегрирования по радиусу в пределах от

до

будем иметь:

Если учесть, что

где

- степень сужения диффузора,

то формулу потерь на трение в диффузоре можно переписать в виде:

Второе слагаемое в формуле потерь напора в диффузоре представляет собой потери энергии на расширение потока.
Эти потери похожи на потери при внезапном расширении

, однако имеют несколько меньшую величину, поэтому в формулу для их определения вводят поправочный коэффициент

. Численное значение этого коэффициента можно определить по формуле Идельчика:

,

или приближённо по формуле Флигнера

.

Окончательно формула для определения потерь напора в диффузоре примет вид

.

Сравнивая это выражение с формулой Вейсбаха легко выявить коэффициент потерь на местном сопротивлении, который для диффузора будет равняться:

Постепенное сужение потока

Такое сопротивление представляет собой коническую сходящуюся трубку – конфузор. Течение в конфузоре сопровождается постепенным увеличением скорости и одновременным снижением давления. По этой причине условия для вихреобразования на конической поверхности отсутствуют. Потери в этой части местного сопротивления происходят только за счёт трения. Вихреобразование может происходить только в узкой части трубы. Его природа аналогична природе подобного вихря при внезапном сужении потока, однако величина существенно меньше. В большинстве работ по гидравлике указывается, что эта величина столь незначительна по сравнению с потерями на трение в конической части конфузора, что ею можно пренебречь.

С учётом сказанного, величину этих потерь можно определить по формуле, вывод которой аналогичен выводу формулы потерь на трение в диффузоре. Она имеет вид:

Выражение для определения коэффициента потерь на трение в конфузоре будет иметь вид:

Поверхностные силы

Поверхностные силы – силы, величины которых пропорциональны площади. К ним относят два вида сил. Силы поверхностного натяжения и силы вязкого трения. Последние проявляются только при движении жидкости и не играют никакой роли, когда жидкость находится в покое. Эти силы, как свойство вязкости, были рассмотрены при изучении свойств жидкостей.

Преобразование уравнений Эйлера

Так же как и в статике, чтобы избавиться от частных производных, умножим эти уравнения соответственно на dx, dy и dz и сложим их:

Проанализируем полученную функцию.

Первые три слагаемые (

) по существу являются суммой инерционных сил или веса, действующих в жидкости. Обозначим эту сумму

и назовём её силовой функцией или точнее силовой потенциальной функцией.

Вспомним из статики, что

- есть полный дифференциал давления dP.

Учтём также, что каждое слагаемое в правой части можно переписать в другом виде. Например,

представить как

. В свою очередь

. И тогда окончательно

. Применив такие же преобразования ко всем трём слагаемым, получим:

С учётом проведённого анализа преобразуем «сложенные уравнения» к обобщённой форме уравнений Эйлера:

Приборы для измерения давления

Существует два основных типа приборов для измерения давления в жидкости.

К приборам первого типа можно отнести пьезометры. Они представляют собой вертикальную трубку, обычно прозрачную. Если, например, нужно измерить давление в точке a, то достаточно подсоединить эту трубку к стенке сосуда так чтобы её конец находился на поверхности равного давления, проходящей через эту точку. В пьезометре установится уровень жидкости, пропорциональный давлению в т. a. Абсолютное давление в этой точке будет

С другой стороны, это же давление можно представить как

Отсюда

Величина

называется пьезометрической высотой. По её величине судят о величине давления.

Если абсолютное давление меньше атмосферного

, то в жидкости имеет место разрежение, или вакуум. Такое давление называют вакуумметрическим давлением

, а высоту в пьезометре называют вакуумметрической высотой

. Эти величины соответственно равны:

Ко второму типу приборов относятся манометры, которые имеют большое разнообразие по типам размерам и характеристикам. Однако принципиально все эти приборы состоят из чувствительного элемента, который меняет свою форму под воздействием давления, и, связанного с этим элементом, передаточного механизма и регистрирующего прибора (индикатора).

Подсоединять манометры для измерения давления в определённой точке надо также как пьезометры, на уровне поверхности равного с выбранной точкой, давления. Например, под действием давления гибкий чувствительный элемент – мембрана изгибается. Размер этого отклонения пропорционален величине измеряемого давления. Вместе с мембраной отклоняется жёстко соединённая с ней стрелка, которая перемещается вдоль шкалы. Такой прибор отличается небольшим отклонением регистрирующего элемента – стрелки, следовательно, точность измерения большой быть не может.

Для увеличения чувствительности прибора мембрану можно соединить с зубчатой рейкой, находящейся в зацеплении с шестерней. Если с последней жёстко соединить стрелку, то при изменении давления она будет поворачиваться по отношению к круговой шкале.
В этом случае изгиб мембраны даст большее, чем в первом случае, линейное отклонение конца стрелки. Это увеличит точность показаний прибора.

Общим недостатком таких приборов является малое исходное отклонение чувствительного элемента – мембраны.

Для устранения этого недостатка используются более сложные чувствительные элементы. Чаще всего таким элементом является полая трубка, согнутая по окружности. Один конец трубки связан со штуцером для подключения к измеряемому давлению, другой с зубчатым сектором, который связан с шестерней и стрелкой, поворачивающейся вокруг шкалы. При повышении давления трубка разгибается, и это отклонение значительно больше, чем отклонение мембраны при таком же давлении.

Во всех случаях чувствительный элемент (мембрану или гибкую трубку) можно связать с индуктивным электрическим преобразователем, состоящим из сердечника и электрической катушки. Можно так же использовать пьезокристаллический преобразователь. В обоих случаях будет генерироваться электрический сигнал, пропорциональный величине давления. Этот сигнал после соответствующих электрических аналоговых или цифровых преобразователей можно передавать на большие расстояния и регистрировать стрелочными или цифровыми, например жидкокристаллическими индикаторами. Этот сигнал несложно также передавать для обработки компьютеру.

Применяемые жидкости

В гидросистемах машин технологического назначения чаще всего применяют специальные жидкости минерального происхождения с диапазоном вязкости при 500С примерно10–175 cСт. Минеральные масла, применяемые в качестве рабочих жидкостей гидросистем, отличаются от минеральных смазочных (машинных) масел тем, что они содержат присадки, придающие им специфические свойства, отсутствующие у смазочных масел. Так, например, для получения минимальной зависимости вязкости от температуры применяют вязкостные присадки.

Прямолинейное равноускоренное движение сосуда с жидкостью

Если сосуд с жидкостью неравномерно движется, то на жидкость действуют силы веса и инерционные силы. Под их действием частицы жидкости принимают новое положение. Если движение равноускоренное, то новое положение оказывается равновесным, и жидкость находится в относительном покое. Свободная поверхность и поверхности уровня не горизонтальные. Форма этих поверхностей определяется величиной и направлением равнодействующей массовых сил. При этом равнодействующая всегда перпендикулярна поверхности (первое свойство гидростатического давления). Поверхности уровня не могут пересекаться, т.к. в этом случае в одной точке действовало бы два разных давления.

Рассмотрим сосуд с жидкостью, движущийся с постоянным ускорением a.

Жидкость в этом сосуде займёт новое равновесное положение. Равновесие объёма жидкости описывается полным дифференциалом давления:

Определим давление в произвольной точке жидкости. Для этого возьмём произвольную точку M на расстоянии l от свободной поверхности. Кроме этого выберем систему координат, такую, что ось Z направлена по перпендикуляру к свободной поверхности. Такое расположение оси не изменит существа вывода, но математические выражения будут проще и более узнаваемы. Тогда при прямолинейном движении в выбранной системе координат:

Подставив эти значения в выражение для полного дифференциала, получим

После интегрирования будем иметь

Постоянную интегрирования C найдём из граничных условий на свободной поверхности, когда при

. Постоянная C примет вид

. После подстановки получим в окончательном виде

Итоговая формула аналогична основному уравнению гидростатики, с той лишь разницей, что вместо глубины h используется расстояние от наклонной свободной поверхности l, а вместо ускорения свободного падения g - равнодействующее ускорение R.

Простые трубопроводы постоянного сечения

Все трубопроводы могут быть разделены на простые и сложные. К простым трубопроводам относятся трубопроводы без разветвлений, а к сложным - трубопроводы, имеющие хотя бы одно разветвление (или место соединения труб).

Пусть простой трубопровод постоянного сечения расположен произвольно в пространстве, имеет общую длину l и диаметр d и содержит ряд местных сопротивлений

. В начальном сечении (1—1) имеем нивелирную высоту Z1 и избыточное давление P1, а в конечном (2—2) — соответственно Z2 и P2. Скорость потока в этих сечениях вследствие постоянства диаметра трубы одинакова и равна V.

Запишем уравнение Бернулли сечений 1—1 и 2—2

;

В этом выражении

- суммарные потери на трение по длине и на местных сопротивлениях на участке трубы длиной l. Потери по длине в соответствии с формулой Дарси будут

Потери на местных сопротивлениях в соответствии с формулой Вейсбаха составят

Учитывая уравнение неразрывности потока и постоянство диаметра трубы т. е.

, скоростные напоры в обеих частях можно сократить. Кроме того величины

, выражающие удельную потенциальную энергию положения, для гидросистем технологического оборудования, как уже не раз отмечалось, много меньше потенциальной энергии сжатия

и отличаются они между собой очень незначительно. По этой причине в дальнейшем их можно не учитывать. Тогда уравнение Бернулли примет вид

или

Выразив величину

через расход

и подставив её в предыдущее выражение, получим

Введём обозначение

Величину

- будем называть гидравлическим сопротивлением трубопровода.

С учётом этого получим

Последнее выражение называется характеристикой трубопровода. Эта характеристика представляет собой зависимость суммарных потерь давления (напора) от расхода в трубопроводе

Если в трубопроводе установлены гидравлические аппараты, имеющие свои сопротивления, то их необходимо добавить к коэффициенту сопротивления трубопровода, и в результате получится суммарное гидравлическое сопротивления.

Протекание гидравлического удара во времени

Рассмотренный ранее процесс распространения ударной волны в трубопроводе не происходит бесконечно долго. В опытах Жуковского было зарегистрировано по 12 полных циклов. При этом величина ударного давления ?P постепенно уменьшалась.

Уменьшение давления вызвано трением в трубе и рассеиванием энергии в резервуаре, обеспечивающем исходный напор. На графике сплошной заштрихованной областью показано теоретическое изменение давления при гидроударе. Прерывистой линией показан примерный вид действительной картины изменения давления.

Распад жидкости под действием различных факторов

Рабочая жидкость в процессе хранения, транспортировки, заправки и эксплуатации подвергается воздействию различных видов энергии, вступает в контакт с различными видами материалов (металлами, полимерами, кислотами, водой и т.д.), многие из которых являются катализаторами химических процессов. Постоянно воздействующим фактором является тепловая энергия, иногда радиационная и электрическая. Эти виды энергии определяют интенсивность статических процессов старения. Старением называют изменение свойств вещества во времени. В динамических условиях, в дополнение к этим видам энергии, на масло действуют механическая энергия при сжатии и разрежении, волновая механическая энергия при вибрациях, звуковых и ультразвуковых колебаниях. В результате этих воздействий в рабочей жидкости происходит комплекс физико-химических изменений, которые можно разделить на три группы.

1. Изменения физического характера: испарение компонентов масла, проникновение в жидкость продуктов изнашивания, растворение газов, воды и компонентов эластомеров, изменение количественного состава присадок за счёт образования сорбционных плёнок на поверхностях контактирующих деталей.

2. Изменения химического характера: окисление углеводородов базового масла и присадок вследствие присутствия в масле воды и водных растворов, реакции присадок масла с материалами гидросистемы и другие химические процессы

3. Изменения механохимического характера: участие масла в процессах трения, перемешивания, а также стимулирующее влияние механических воздействий на химические реакции.

Растворение газов

Растворение газов - способность жидкости поглощать (растворять) газы, находящиеся в соприкосновении с ней. Все жидкости в той или иной степени поглощают и растворяют газы. Это свойство характеризуется коэффициентом растворимости kр.

Если в закрытом сосуде жидкость находится в контакте с газом при давлении P1, то газ начнёт растворяться в жидкости. Через какое-то время

произойдёт насыщение жидкости газом и давление в сосуде изменится. Коэффициент растворимости связывает изменение давления в сосуде с объёмом растворённого газа и объёмом жидкости следующим соотношением

где WГ – объём растворённого газа при нормальных условиях,

Wж – объём жидкости,

P1 и P2 – начальное и конечное давление газа.

Коэффициент растворимости зависит от типа жидкости, газа и температуры.

При температуре 20 ºС и атмосферном давлении в воде содержится около 1,6% растворенного воздуха по объему (kp = 0,016). С увеличением температуры от 0 до 30 ºС коэффициент растворимости воздуха в воде уменьшается. Коэффициент растворимости воздуха в маслах при температуре 20 ºС равен примерно 0,08 – 0,1. Кислород отличается более высокой растворимостью, чем воздух, поэтому содержание кислорода в воздухе, растворенном в жидкости, примерно на 50% выше, чем в атмосферном. При уменьшении давления газ из жидкости выделяется. Процесс выделения газа протекает интенсивнее, чем растворение.

Разновидности гидроудара

Если трубопровод перекрыть не полностью, то скорость жидкости изменится не до нуля, а до значения V1 . В этом случае может возникнуть неполный гидроудар, при котором величина повышения давления (ударное давление) будет меньше, чем в первом случае, а формула Жуковского примет вид

Приведённые формулы справедливы только в том случае, если время закрытия крана tЗАК меньше фазы гидравлического удара

, т.е.

В том случае, если

, возникает непрямой гидроудар. Для него характерно то, что отразившаяся от резервуара в начале трубы ударная волна возвращается к заслонке крана раньше, чем он будет полностью закрыт. Величина

Р в этом случае будет меньше, чем при прямом гидроударе. Её приближенно (считая, что изменение Р в трубопроводе происходит по линейному закону) можно определить по формуле:

В гидроприводах технологических машин, станков и т.п. очень часто возникает так называемый гидроудар в тупиковом трубопроводе. В этом случае возможно увеличение ударного давления в два раза. Пояснить это можно следующим рисунком.

Трубопровод с низким начальным давлением отделён от источника гидравлической энергии высокого давления. При мгновенном (в реальных гидросистемах 0,008 – 0,001с) открытии заслонки крана давление в начале трубопровода внезапно возрастает на величину

Р =Р1 - РО.

Возникает волна повышенного давления, которая движется к концу трубопровода со скоростью а. Скорость же движения жидкости становится равной

, а давление отличается от Р0 на величину

Р. В момент времени

волна достигнет тупика, и вся труба окажется расширенной.

Т.к. дальнейшее движение жидкости невозможно, то передние её слои остановятся, а последующие по инерции будут набегать на них. Это вызовет дополнительное повышение давления в конце трубы на величину

Р. Возникнет вторая, отражённая волна, которая движется к началу трубопровода со скоростью а. Давление за фронтом ударной волны становится Р2 =Ро+2

Р, а скорость жидкости V=0.

Далее весь процесс продолжается как в случае полного гидроудара, но колебания давления происходят относительно величины Р1=Ро+

Р, а не относительно Ро.

Разветвлённые трубопроводы

Разветвлённые трубопроводы отличаются тем, что они имеют одну общую точку, из которой расходятся разные потоки, или общую точку, в которой несколько разных потоков сходится. Этот вариант наиболее часто встречается в гидросистемах технологического оборудования, где от одной насосной станции питается сразу несколько одновременно работающих потребителей. Для разветвлённых трубопроводов, так же как и для параллельных, можно записать уравнение расходов

где

- расходы в соответствующих ветвях.

Составим также уравнение Бернулли для любой из ветвей. Будем считать: давление в трубопроводе таково, что нивелирной высотой можно пренебречь. Примем также, что давление в конце каждой ветви (в сечении к), необходимое для преодоления нагрузки, равно

. Уравнение Бернулли для сечений н и к будет выглядеть следующим образом:

где i – индекс, соответствующий определённой ветви.

Если считать, что рассматриваемая система трубопроводов принадлежит гидросистеме технологической машины, в которой давления в различных ветвях, как правило, составляют несколько мегапаскалей, а скорости течения жидкости по трубам чаще всего невысокие (до5 м/c), скоростным напором можно пренебречь. В самом деле, например, при скорости 1 м/c и коэффициенте кинетической энергии ? равным 2, величина скоростного напора составит 0,1 м, что при переводе в единицы давления равно 0,001МПа. С учетом этого и после обычных преобразований получим

Величина

, в данном случае, представляет собой характеристику простого трубопровода и равна

. Таким образом, для каждой ветви разветвлённого трубопровода можно написать подобное уравнение. Если добавить к ним уравнение расходов, то можно получить систему уравнений вида

Подобную систему уравнений можно записать для любого числа ветвей разветвлённого трубопровода. Решая её, можно определить, какой расход и какое давление должен обеспечивать источник гидравлической энергии, чтобы на выходе трубопроводов получалось заданное давление при заданном расходе.

Сила давления жидкости на криволинейную стенку

Чаще всего необходимо определить силу, действующую на цилиндрическую поверхность, имеющую вертикальную ось симметрии. Возможны два варианта. Первый вариант - жидкость воздействует на стенку изнутри.

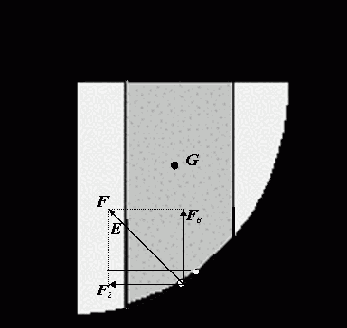
Во втором варианте жидкость действует на стенку снаружи. Рассмотрим оба этих варианта.

В первом случае выделим объём жидкости, ограниченный рассматриваемым участком цилиндрической поверхности AB, участком свободной поверхности CD, расположенным над участком AB, и двумя вертикальными поверхностями BC и CD, проходящими через точки A и B. Эти поверхности ограничивают объём ABCD, который находится в равновесии. Рассмотрим условия равновесия этого объёма в вертикальном и горизонтальном направлениях. Заметим, что, если жидкость действует на поверхность AB, c какой то силой F, то с такой же силой, но в обратном направлении, и поверхность действует на рассматриваемый объём жидкости. Эту силу, перпендикулярную поверхности AB, можно представить в виде горизонтальной Fг и вертикальной Fв составляющих.

Условие равновесия объёма ABCD в вертикальном направлении выглядит, так:

;

где P0 – внешнее давление,

Sг – площадь горизонтальной проекции поверхности AB,

G – вес выделенного объёма жидкости.

Условие равновесия этого объёма в горизонтальной плоскости запишем с учётом того, что силы, действующие на одинаковые вертикальные поверхности AD и CE, взаимно уравновешиваются. Остаётся только сила давления на площадь BE, которая пропорциональна вертикальной проекции Sв поверхности AB. С учётом частичного уравновешивания будем иметь условие равновесия сил в горизонтальном направлении в виде:

где hс- глубина расположения центра тяжести поверхности AB.

Зная Fг и Fв определим полную силу F, действующую на цилиндрическую поверхность

Во втором случае, когда жидкость воздействует на цилиндрическую поверхность снаружи, величина гидростатического давления во всех точках поверхности AB имеет те же значения, что и в первом случае, т.к. определяется такой же глубиной. Силы, действующие на поверхность в горизонтальном и вертикальном направлениях, определяются по тем же формулам, но имеют противоположное направление. При этом под величиной G надо понимать тот же объём жидкости ABCD, несмотря на то, что на самом деле он, в данном случае и не заполнен жидкостью.

Положение центра давления на цилиндрической стенке легко можно найти, если известны силы Fг и Fв и определены центр давления на вертикальной проекции стенки и центр тяжести рассматриваемого объёма ABCD. Задача упрощается, если рассматриваемая поверхность является круговой, т.к. равнодействующая сила при этом пересекает ось поверхности. Это происходит из-за того, что силы давления всегда перпендикулярны поверхности, а перпендикуляр к окружности всегда проходит через её центр.

Сила давления жидкости на плоскую стенку

Рассмотрим произвольную площадку ds, расположенную на плоской наклонной стенке сосуда с жидкостью на расстоянии Y от оси X, и определим силы, действующие на эту площадку. Сила от давления, действующего на элементарную площадку dS, будет описываться формулой:

Если проинтегрировать это выражение по площади, можно определить полную силу, действующую на всю площадь целиком

Из рисунка ясно, что в последнем выражении

. Подставив значение h в предыдущее выражение, будем иметь:

Из теоретической механики известно, что интеграл

есть ни что иное, как статический момент площади S относительно оси 0X. Он равен произведению этой площади на координату её центра тяжести, т.е. можно записать

где Yс – расстояние от оси X до центра тяжести площади S.

Подставив формулу момента в выражение силы, получим:

Анализ второго слагаемого показывает, что произведение

это глубина положения центра тяжести площадки, а

- избыточное давление жидкости в центре тяжести площадки. С учётом этого можно записать

Сумма в скобках в последнем выражении является абсолютным давлением в центре тяжести рассматриваемой произвольной площадки. Таким образом, можно сделать вывод: полная сила давления жидкости на плоскую стенку равна произведению её площади на величину гидростатического давления в центре тяжести этой стенки.

Однако необходимо учесть, что эта сила не сконцентрирована в точке, а распределена по площади. И распределение это неравномерно. По этой причине для расчётов, кроме величины силы действующей на наклонную площадку, необходимо знать точку приложения равнодействующей.

Силы давления

Давление – напряжение, возникающее в жидкости под действием сжимающих сил.

В общем случае поверхностная сила

, действующая на площадке

под некоторым углом к ней, может быть разложена на нормальную

и тангенциальную

составляющие. Первая, направленная внутрь объема, называется силой давления, вторая – силой трения. Нормальная составляющая вызывает в жидкости нормальные напряжения или гидромеханическое давление, которое в покоящейся жидкости называется гидростатическим. Если сила

равномерно распределена по площадке

, то

или переходя, к пределу

В любом случае причиной возникновения давления является внешняя сила, приложенная к жидкости. Часто в гидроприводе такой силой является нагрузка F, приложенная к исполнительному органу. Эта нагрузка воздействует на жидкость через какую-то жёсткую поверхность и, следовательно, распределена равномерно, например площадь поршня гидроцилиндра S. В таком случае давление P определяется по формуле

Если давление отсчитывается от нуля, оно называется абсолютным и обозначается

, если от атмосферного, – избыточным и обозначается

. Атмосферное давление обозначается

Кроме того, различают давление гидродинамическое и гидростатическое. Гидродинамическое давление возникает в движущейся жидкости. Гидростатическое давление – давление в покоящейся жидкости.

Силы поверхностного натяжения

Молекулы жидкости притягиваются друг к другу с определённой силой. Причём внутри жидкости силы, действующие на любую молекулу, уравновешиваются, т.к. со всех сторон от неё находятся одинаковые молекулы, расположенные на одинаковом расстоянии. Однако молекулы жидкости, находящиеся на границе (с газом, твердым телом или на границе двух несмешивающихся жидкостей) оказываются в неуравновешенном состоянии т.к. со стороны другого вещества действует притяжение других молекул, расположенных на других расстояниях. Возникает преобладание какой-то силы. Под влиянием этого воздействия поверхность жидкости стремится принять форму, соответствующую наименьшей площади. Если силы внутри жидкости больше наружных сил, то поверхность жидкости стремится к сферической форме. Например, малые массы жидкости в воздухе стремятся к шарообразной форме, образуя капли. Может иметь место и обратное явление, которое наблюдается как явление капиллярности. В трубах малого диаметра (капиллярах) наблюдается искривление свободной поверхности, граничащей с газом или с парами этой же жидкости. Если поверхность трубки смачивается, свободная поверхность жидкости в капилляре вогнутая. Если нет смачивания, свободная поверхность выпуклая, как при каплеобразовании. Во всех этих случаях силы поверхностного натяжения обусловливают дополнительные напряжения pпов в жидкости. Величина этих напряжений определяется формулой

где ? - коэффициент поверхностного натяжения,

r - радиус сферической поверхности, которую принимает жидкость.

Эти дополнительные напряжения легко наблюдать, если в сосуд с жидкостью погрузить капилляр. В этом опыте возможны два варианта. В первом случае жидкость, за счёт поверхностных сил, поднимется по капилляру на некоторую высоту. Тогда говорят о капиллярном поднятии, и наблюдается явление смачивания.

Во втором варианте жидкость опускается в капилляре ниже уровня жидкости в сосуде. Такое явление называют капиллярным опусканием, которое происходит при несмачивании.

В обоих случаях величина

пропорциональна дополнительному напряжению, вызванному в жидкости поверхностными силами.
Она равна

;

где ? - коэффициент поверхностного натяжения,

d – диаметр капилляра,

k – коэффициент пропорциональности, который выражается следующей формулой

,

и зависит от жидкости. Например, при t = 20 ºC, k спирта составляет 11,5, ртути –10,15 а воды - 30.

Поднятие воды в капиллярах почвы и грунтов является важным фактором в распространении воды. Высота капиллярного поднятия в грунтах изменяется от нуля (галечники) почти до 5 м (глины). При этом с увеличением минерализации воды высота капиллярного поднятия увеличивается.

Поверхностное натяжение и капиллярные эффекты определяют закономерности движения жидкости в условиях невесомости.

К поверхностным силам относятся и силы давления, т.к. они действуют на поверхности жидкости.

Скорость распространения гидравлической ударной волны в трубопроводе

Изменения давления и скорости потока в трубопроводах происходят не мгновенно в связи с упругостью твёрдых стенок трубы и сжимаемостью рабочей среды, а с некоторой конечной скоростью, обусловленной необходимостью компенсации упругих деформаций жидкости и трубы. Рассмотрим случай когда в трубопроводе длиной L и площадью сечения ? под давлением Р находится жидкость, плотность которой ?. Предположим, что в момент времени t в сечении 1 – 1 давление повысится на величину dp. Это повышение вызывает увеличение плотности на величину d?, а также расширение внутреннего диаметра трубы. Следовательно, площадь проходного сечения увеличится на величину d?. В результате увеличится объём W участка трубы на величину dW. За счёт этого произойдет увеличение массы жидкости находящейся в трубе на участке длиной L. Масса увеличится за счёт увеличения, во-первых, плотности жидкости, во-вторых, за счёт увеличения объёма W.

Такая ситуация рассматривалась при выводе уравнения неразрывности потока в дифференциальной форме, с той только разницей, что там рассматривалось лишь изменение массы во времени, без учёта вызвавших это изменение причин

. По аналогии с приведённым уравнением запишем выражение, описывающее изменение массы за счёт изменения давления

Жидкость под действием указанного повышения давления устремится с некоторой скоростью а в слои с меньшим давлением, в которых также будет повышаться плотность и увеличиваться напряжение в стенках трубопровода, способствующее увеличению площади трубопровода. В связи с этим потребуется некоторое время на распространение этих деформаций вдоль трубопровода.

С другой стороны, перемещение массы dm за время dt происходит под влиянием результирующей Fр сил давления, действующих вдоль линии движения на торцовые поверхности цилиндрического объёма длиной L

В этом случае уравнение импульса силы может быть представлено в следующем виде

Отсюда

Имея в виду, что

, и подставив это в предыдущее выражение, получим

Заметим, что произведение

Приравняем оба выражения для

и получим:

.

Выразим из последнего равенства величину a2

Разделим числитель и знаменатель на W, а первое слагаемое в знаменателе искусственно умножим и разделим на ?:

.

Обратим внимание на то, что

. После подстановки этих равенств в последнее выражение и извлечения корня получим выражение для скорости распространения ударной волны, которая, по сути, является скоростью распространения упругих деформаций жидкости в трубе.

Здесь первое слагаемое под корнем характеризует упругие свойства рабочей среды (жидкости), а – второе упругие силы материала трубы.

Рассмотрим подробнее эти слагаемые.

Как известно из гидростатики, сила, действующая на цилиндрическую поверхность, равна произведению давления на проекцию площади этой поверхности в направлении действия силы. На рассматриваемый участок трубы с толщиной стенок ?, длиной L и диаметром D действует изнутри давление P. Вследствие этого возникает разрывающая сила F, равная

.

В стенках трубы возникает сила сопротивления

, равная произведению площади сечения стенок трубы

на внутренние напряжения

в материале стенок трубы, т.е.

.

Если приравнять две эти силы, получим равенство

,

из которого найдём выражение, определяющее внутреннее напряжение в стенках трубы

Полагая, что относительное увеличение диаметра трубы, равное

, прямо пропорционально напряжению в стенках трубы, можно записать

где Ет - коэффициент пропорциональности, который является модулем упругости материала трубы.

Из двух последних выражений следует, что абсолютное приращение радиуса сечения трубы может быть выражено формулой

Запишем выражение, определяющее увеличение площади сечения трубы:

где ? – начальная площадь сечения трубы,

?р – площадь сечения трубы при давлении P.

Пренебрегая малой величиной высшего порядка ?R2 и подставив выражение для ?R, получим

Продифференцировав это выражение по P и рассматривая ? как функцию, зависящую от P, получим:

В итоге слагаемое, описывающее упругие свойства материала трубы в выражении для скорости распространения ударной волны, можно представить в следующем виде:

Теперь рассмотрим слагаемое, описывающее упругость жидкости

. Ранее при рассмотрении свойств жидкости было установлено, что если изменение объёма происходит за счёт изменения плотности, то можно определить коэффициент сжимаемости жидкости ?w:

Часто этот коэффициент выражают через обратную величину, называемую модулем упругости жидкости Eж, т. е.:

Отсюда следует, что второе слагаемое, характеризующее упругие свойства рабочей среды, может быть представлено в виде:

Таким образом, окончательно выражение для скорости распространения ударной волны в упругом трубопроводе можно переписать в следующем виде:

где

- плотность жидкости,

D - диаметр трубопровода,

- толщина стенки трубопровода,

Ет – объёмный модуль упругости материала трубы,

Еж - объёмный модуль упругости жидкости.

Из формулы следует, что скорость распространения ударной волны зависит от сжимаемости жидкости и упругих деформаций материала трубопровода.

Следствия основного уравнения гидростатики

Во-первых, из основного уравнения гидростатики следует, что для любой точки жидкости в состав величины давления входит P0 - давление, которое приложено к граничной поверхности жидкости извне. Эта составляющая одинакова для любой точки жидкости. Поэтому из основного уравнения гидростатики следует закон Паскаля, который гласит: давление, приложенное к граничной поверхности покоящейся жидкости, передаётся всем точкам этой жидкости по всем направлениям одинаково. Следует подчеркнуть, что давление во всех точках не одинаково. Одинакова лишь та часть (составляющая), которая приложена к граничной поверхности жидкости. Закон Паскаля – основной закон, на основе которого работает объёмный гидропривод, применяемый в абсолютном большинстве гидросистем технологических машин.

Вторым следствием является тот факт, что на равной глубине в покоящейся жидкости давление одинаково. В результате можно говорить о поверхностях равного давления. Для жидкости, находящейся в абсолютном покое или равномерно движущейся, эти поверхности – горизонтальные плоскости. В других случаях относительного покоя, которые будут рассмотрены ниже, поверхности равного давления могут иметь другую форму или не быть горизонтальными. Существование поверхностей равного давления позволяет измерять давление в любой точке жидкости.

Смазочный слой в подшипнике

Особым случаем ламинарного движения жидкости в кольцевом зазоре является относительное вращение двух цилиндрических поверхностей, образующих кольцевую щель между вращающейся цапфой и неподвижным вкладышем.

За счёт вращения цапфы и прилипания к её поверхности жидкости образуется гидравлический клин, в котором развивается гидродинамическое давление, порождающее силу, уравновешивающую силы нагрузки, действующее на цапфу. Такие устройства широко применяются в технике и называются подшипниками скольжения. Математическое описание, применяемое для плоских щелей, к данному случаю не подходит, т.к. величина зазора по направлению движения не постоянна, а движение жидкости в подшипнике описывается значительно более сложными уравнениями. Поэтому в рамках настоящего курса мы коснёмся только основных результатов теории подшипников скольжения жидкостного трения. Она основана на гидродинамической теории смазки, которая была разработана русским учёным Петровым Н. П. в 1883г. Ему же принадлежит первая теоретическая формула для коэффициента трения подшипника скольжения.

В результате совместного решения шести уравнений равновесия для вязкой жидкости, уравнения неразрывности и трёх уравнений движения, с учётом ряда допущений, получено основное дифференциальное уравнение гидродинамической теории смазки:

где

- гидродинамическое давление,

- динамическая вязкость,

- толщина плёнки жидкости,

- радиус цапфы,

- окружная скорость цапфы,

- текущее значение угла, в котором определяется давление,

- координата, отсчитываемая от середин вкладыша в осевом направлении.

Расчётная схема подшипника скольжения показана на рисунке, где использованы следующие обозначения:

- диаметр цапфы,

- диаметр вкладыша,

- эксцентриситет между осями цапфы и вкладыша,

- минимальная толщина плёнки жидкости,

- толщина плёнки жидкости в области максимального давления,

- угловая координата,

- значения углов начала и конца эпюры давления относительно линии центров.

Без учёта торцовых утечек жидкости основное уравнение гидродинамической теории смазки упрощается и принимает вид:

,

где

- давление в любой точке щели для бесконечно длинного подшипника.

Для подшипника конечной длины

справедливо уравнение, определяющее давление ?:

.

Касательное напряжение на цапфе ? равно:

.

Несущая способность (грузоподъёмность) W подшипника:

.

Сила трения

и расход жидкости

определяются уравнениями

.

Решение последних уравнений затруднено сложными зависимостями изменения давления в слое жидкости по углу

и по длине цапфы для определённых геометрических размеров подшипника.

На практике для расчёта подшипников скольжения используют диаграммы безразмерных коэффициентов

,

где

- коэффициент нагруженности подшипника,

;

- коэффициент сопротивления цапфы вращению,

;

- потеря мощности на преодоление сил сопротивления вращению цапфы в подшипнике;

- коэффициент торцового расхода,

;

- относительный зазор,

;

- относительная длина подшипника,

;

- относительный эксцентриситет,

;

- средний зазор,

;

- угловая скорость вращения цапфы.

Сопротивление потоку жидкости

Гидравлическая жидкость в гидросистемах технологического оборудования, как уже обсуждалось ранее, играет роль рабочего тела. Она обеспечивает перенос энергии от источника гидравлической энергии к потребителю (в большинстве случаев, к гидродвигателю). Для такого переноса используются напорные потоки. В подобных потоках жидкость со всех сторон ограничена твёрдыми стенками трубопроводов, каналов гидроаппаратов и полостей гидромашин. В дальнейшем мы будем ориентироваться именно на такие случаи, хотя аналогичные процессы сопровождают и движение безнапорных потоков.

Естественно, что твёрдые стенки препятствуют свободному движению жидкости. Поэтому при относительном движении жидкости и твердых поверхностей неизбежно возникают (развиваются) гидравлические сопротивления. На преодоление возникающих сопротивлений затрачивается часть энергии потока. Эту потерянную энергию называют гидравлическими потерями удельной энергии или потерями напора. Гидравлические потери главным образом связаны с преодолением сил трения в потоке и о твёрдые стенки и зависят от ряда факторов, основными из которых являются:

ü геометрическая форма потока,

ü размеры потока,

ü шероховатость твёрдых стенок потока,

ü скорость течения жидкости,

ü режим движения жидкости (который связан со скоростью, но учитывает её не только количественно, но и качественно),

ü вязкость жидкости,

ü некоторые другие эксплуатационные свойства жидкости.

Но гидравлические потери практически не зависят от давления в жидкости.

Величина гидравлических потерь оценивается энергией, потерянной каждой весовой единицей жидкости. Из уравнения Бернулли, составленного для двух сечений потока, обозначенных индексами 1 и 2 потери энергии потока жидкости

можно представить как

Напомним, что в этом уравнении

- энергия единицы веса жидкости, движущейся в поле сил тяготения,

- потенциальная энергия единицы веса жидкости, зависящая от её положения над уровнем нулевого потенциала (линией отсчёта),

- потенциальная энергия единицы веса жидкости, зависящая от степени её сжатия (от давления),

- давление в потоке жидкости,

- плотность жидкости,

- кинетическая энергия единицы веса потока жидкости,

- коэффициент кинетической энергии,

- средняя скорость потока жидкости,

- ускорение свободного падения.

Если учесть, что труба в обоих сечениях 1 и 2 имеет одинаковые площади поперечных сечений, жидкость является несжимаемой и выполняется условие сплошности (неразрывности) потока, то, несмотря на гидравлические сопротивления и потери напора, кинетическая энергия в обоих сечениях будет одинаковой. Учтя это, а также то, что при больших давлениях в напорных потоках и небольшой (практически нулевой) разнице нивелирных высот Z1 и Z2, потери удельной энергии можно представить в виде

.

Опыты показывают, что во многих (но не во всех) случаях потери энергии прямо пропорциональны квадрату скорости течения жидкости, поэтому в гидравлике принято выражать потерянную энергию в долях от кинетической энергии, отнесённой к единице веса жидкости

,

где

- коэффициент сопротивления.

Таким образом, коэффициент сопротивления можно определить как отношение потерянного напора к скоростному напору.

Гидравлические потери в потоке жидкости разделяют на 2 вида:

Ø потери по длине,

Ø местные потери.

Сопротивление растяжению жидкостей

Сопротивление растяжению жидкостей заключается в способности жидкости противостоять растягивающим силам.

Сопротивление растяжению жидкостей может возникать только в дегазированных жидкостях. В опытах удавалось при центрифугировании дегазированной дистиллированной воды получить на очень короткое время напряжения растяжения в воде, доходившие приблизительно до 25 МПа. Технические жидкости не сопротивляются растягивающим усилиям.

Газы могут находиться в жидкости в растворенном и нерастворенном виде. Присутствие в жидкости нерастворенного газа в виде пузырьков существенно уменьшает модуль упругости жидкости, причем это уменьшение не зависит от размеров пузырьков воздуха. Динамическая вязкость жидкости с увеличением содержания в ней воздуха растет. Содержание нерастворенного воздуха в рабочих жидкостях гидросистем машин и механизмов, так же как и в трубопроводах, подающих жидкость, может сильно повлиять на параметры работы трубопроводов и гидросистем.

Список литературы

1. Башта Т.М. Гидравлика, гидравлические машины и гидравлические приводы.– М.: Машиностроение, 1970г.-504 с.

2. Башта Т.М. Машиностроительная гидравлика.- М.: Машиностроение, 1971г.-672 с.

3. Орлов Ю.М. Механика жидкости, гидравлические машины и основы гидропривода агрегатов ракетных комплексов. Учебное пособие. – М: ООО «Пресс-мастер», 2001.- 379с.

4. Иванов В.И., Навроцкий В.К., Сазанов И.И., Трифонов О.Н. Гидравлика и объемный гидропривод. Учебное пособие. - М.: ИЦ МГТУ «СТАНКИН», 2003. – 154 с.

5. Шейпак А.А. Гидравлика и гидропневмопривод: Учебное пособие. Ч1. Основы механики жидкости и газа. 2-е изд. Перераб. и доп. –М.: МГИУ, 2003. –192с.

6. Схиртладзе А.Г., Иванов В.И., Кареев В.Н. Гидравлические и пневматические системы.– М.: ИЦ МГТУ “Станкин”, Янус-К, 2003. –544с.

7. Станочные гидравлические системы. Под ред. Ф.Ю. Свитковского. – Ижевск-Екатеринбург, изд. Института экономики Ур. РАН., 2003. 239с.

8. Избаш С.В. Основы гидравлики. – М.: Государственное издательство литературы по строительству и архитектуре, 1952. 423с.

9. Чугаев Р.Р., Гидравлика: Учебник для вузов. – 4-е изд. доп. и перераб. - Л. Энергоиздат. Ленингр. отд-ние, 1982. 672с.

Струйная модель потока

В гидравлике рассматривается струйная модель движения жидкости, т.е. поток представляется как совокупность элементарных струек жидкости, имеющих различные скорости течения u?. Индекс ? означает (напоминает), что в каждой точке живого сечения скорости различны. Элементарные струйки как бы скользят друг по другу. Они трутся между собой и вследствие этого их скорости различаются. Причём, в середине потока скорости наибольшие, а к периферии они уменьшаются. Распределение скоростей по живому сечению потока можно представить в виде параболоида с основанием, равным ?. Высота его в любой точке равна скорости соответствующей элементарной струйки u?. Площадь элементарной струйки равна d?. В пределах этой площади скорость можно считать постоянной. Понятно, что за единицу времени через живое сечение потока будет проходить объём жидкости Wt, равный объёму параболоида. Этот объём жидкости и будет равен расходу потока.

С учётом понятия средней скорости, которая во всех точках живого сечения одинакова, за единицу времени через живое сечение потока будет проходить объём жидкости (обозначим его Wtср ), равный:

Wtср =?Vср.

Если приравнять эти объёмы Wtср = Wt=параболоида, можно определить значение средней скорости потока жидкости:

В дальнейшем среднюю скорость потока жидкости будем обозначать буквой V без индекса ср.

При неравномерном движении средняя скорость в различных живых сечениях по длине потока различна. При равномерном движении средняя скорость по длине потока постоянна во всех живых сечениях.

Свойства гидростатического давления

Первое свойство формулируется следующим образом: на внешней поверхности жидкости гидростатическое давление всегда направлено по нормали внутрь рассматриваемого объёма.

В приведённой формулировке «внешняя поверхность» это любая поверхность, которую можно выделить внутри жидкости (даже мысленно), или поверхность раздела сред.

Доказывается первое свойство путём рассуждений методом «от противного».

Рассмотрим покоящуюся жидкость. Известно, что жидкость плохо сопротивляется касательным усилиям. Если бы сила, от давления R действовала бы не по нормали к площадке, то её можно было бы представить в виде двух составляющих – нормальной Fn и касательной F?. Тогда касательная составляющая смещала бы слои жидкости друг относительно друга. Это означало бы, что жидкость не находилась бы в покое. Это противоречит начальному утверждению.

Из первого свойства следует, что напряжение сжатия - единственный вид напряжений в покоящейся жидкости

Второе свойство состоит в том, что в любой точке внутри жидкости давление по всем направлениям одинаково. Иначе это свойство давления звучит так: на любую площадку внутри объёма жидкости, независимо от её угла наклона, действует одинаковое давление.

Докажем второе свойство. Для этого рассмотрим произвольный объём в неподвижной жидкости в виде прямоугольного тетраэдра с размерами

. Будем рассматривать этот объём в некоторой произвольной системе координат X,Y,Z.

На рисунке приведены следующие буквенные обозначения:

- гидростатическое давление, действующее на грань, перпендикулярную соответствующей оси,

- гидростатическое давление, действующее на наклонную грань dS,

F- инерционные силы (или силы веса).

Тетраэдр dx, dy, dz по определению находится в покое, следовательно, сумма сил, действующих на него равна 0, т.е.

Подробно рассмотрим эти силы. Прежде всего, на выделенный тетраэдр действуют силы давления. В проекциях на оси системы координат по направлению каждой из осей действует сила от давления на грань, перпендикулярную этой оси.
Этой силе противодействует проекция на соответствующую ось силы давления на наклонную (большую) грань тетраэдра. Получаются три пары сил, соответственно осям:

Вместе с силами давления, в общем случае, на тетраэдр действуют инерционные силы (или в простейшем случае сила веса), которые равны произведению массы на проекцию ускорения на соответствующую ось. Массу определим как произведение плотности жидкости и объёма тетраэдра. Объём для прямоугольного тетраэдра равен

. В этом случае инерционные силы примут вид:

.
Сложив обе полученные системы уравнений, и, приравняв их 0 по причине равновесия тетраэдра, получим общую систему уравнений сил, действующих в покоящейся жидкости:

Если учесть, что площадь каждой грани тетраэдра, параллельной плоскостям координат, равна площади проекции наклонной грани на соответствующую координатную плоскость, получим следующее равенство:

.
Разделив уравнения сил на соответствующие одинаковые площади, получим:

.
Устремив размеры тетраэдра к 0, т.е.

последняя система уравнений примет вид:

.
Приравняв все три уравнения, получим следующее равенство:

.
В результате можно сделать следующий вывод: давление не зависит от направления, или другими словами: давление - величина скалярная.
Однако возникает вопрос, каким образом получается, что давление и площадь величины скалярные, а их произведение сила – величина векторная.

.
Ответ на этот вопрос заключается в следующем. Направление вектора силы задаёт площадка, на которую действует давление. Это направление всегда перпендикулярно площадке действия и направлено внутрь рассматриваемого объёма.

Сжатие струи

При вытекании жидкости из резервуара через отверстие в тонкой стенке, диаметр которого значительно меньше размеров резервуара, а края отверстия имеют прямоугольную форму, диаметр вытекающей струи будет меньше размеров диаметра отверстия. Это происходит потому, что жидкость, вытекающая из резервуара, попадает в отверстие со всех направлений, а после прохождения отверстия направление движения всех частиц жидкости становится одинаковым. Изменение направления движения частиц жидкости в силу их инерционности мгновенно произойти не может. Поэтому сжатие струи обусловлено необходимостью постепенного изменения направления движения жидкости при прохождении отверстия. Так как размеры резервуара много больше размеров отверстия, боковые поверхности и свободная поверхность не могут оказывать влияния на направление входа жидкости в отверстие, то в этом случае наблюдается совершенное сжатие струи. Такое сжатие является наибольшим, и оно достигается на расстоянии примерно равном диаметру отверстия. Степень сжатия выражается коэффициентом сжатия

где

- площадь и диаметр отверстия,

- площадь и диаметр совершенно сжатой струи.

В том случае, если истечение происходит из резервуара такой формы, что его стенки влияют на траекторию движения частиц при входе в отверстие, наблюдается несовершенное сжатие струи.

Вследствие того, что боковые стенки резервуара перед отверстием формируют направление движения жидкости, струя после отверстия сжимается в меньшей степени, чем при вытекании из практически бесконечного резервуара. По этой причине меняется коэффициент сжатия струи. Формулы для определения этого сжатия для разных жидкостей и разных условий истечения - эмпирические. Например, для круглого центрального отверстия в тонкой торцовой стенке трубы и для маловязких жидкостей коэффициент сжатия

можно находить по следующей эмпирической формуле в долях от коэффициента сжатия

при совершенном сжатии струи

;

где

;

где, в свою очередь,

- площадь отверстия,

- площадь сечения резервуара (в приведённом примере площадь поперечного сечения трубы).

Сжимаемость жидкости

Сжимаемость жидкости это свойство жидкостей изменять свой объём при изменении давления.

Сжимаемость характеризуется коэффициентом объёмного сжатия (сжимаемости) ?P, представляющим собой относительное изменение объёма жидкости W при изменении давления P на единицу.

Знак минус в формуле указывает, что при увеличении давления объём жидкости уменьшается.

Единицы измерения: Па-1 (Паскаль. 1Па=1Н/м2).

Перепишем определение

в виде

Обе части умножим на знаменатель и перенесём в левую часть

Учтём, что

и подставим в предыдущее равенство

Выразив отсюда W, можно получить формулу для вычисления нового значения объёма при известном увеличении давления

Если учесть, что все изменения объёма происходят при неизменной массе за счёт изменения плотности (

), можно получить формулу изменения плотности при изменении давления

Откуда выразив ?, получим

Изменение объёма dW, происходящее за счёт изменения плотности d? при постоянной массе, можно записать в виде

Подставив это в определение ?P, определим коэффициент сжимаемости жидкости через изменение плотности

Отсутствие знака минус в этом выражении означает, что увеличение давления приводит к увеличению плотности.

Величина, обратная коэффициенту сжимаемости, или, по-другому, коэффициенту объёмного сжатия

, обозначается

и называется объёмным модулем упругости жидкости.

Тогда предыдущая формула примет вид

Это выражение называется законом Гука для жидкости.

Единицы измерения: [Па], [МПа], [кГс/ см2].

Модуль упругости Еж зависит от температуры и давления. Поэтому различают два модуля упругости: адиабатический и изотермический. Первый имеет место при быстротекущих процессах без теплообмена. Процессы, происходящие в большинстве гидросистем, происходят с теплообменом, поэтому чаще используется изотермический модуль упругости. Примерная форма зависимостей Eж от P и t0 представлена на графиках. Всё это говорит о том, что жидкости не вполне точно следуют закону Гука.

Приведём несколько примеров значений модулей упругости.

Минеральные масла, используемые в технологических машинах с гидравлическим приводом, при t0 = 20 оC имеют объёмные модули упругости 1,35·103 ÷ 1,75·103 МПа (меньшее значение относится к более легкому маслу), бензин и керосин – приблизительно 1,3·103 МПа, глицерин - 4,4·103 МПа, ртуть – в среднем 3,2·103 МПа.

В практике эксплуатации гидравлических систем имеются случаи, когда вследствие действия того или иного возмущения в жидкости может значительно изменяться давление. В таких случаях пренебрежение сжимаемостью приводит к существенным погрешностям.

Известно, что скорость распространения звука с в однородной жидкости можно определить по формуле

Если вспомнить, что

, и подставить это значение в формулу скорости распространения звука, получим

В этом случае изменение плотности жидкости, вызванное изменением давления, будет

Если считать, что жидкость несжимаемая, т.е. dr = 0, то окажется, что скорость распространения звука в жидкости по приведённой формуле окажется бесконечной (c = ¥). При использовании такого значения c в случае достаточно больших объёмов жидкости (озеро или нефтепровод) или быстрого изменения давления, например, при резком закрытии или открытия запорного устройства в трубопроводе, результаты расчётов окажутся существенно неточными. По этой причине в описанных условиях принимать жидкость несжимаемой недопустимо.

Течение при больших перепадах давления

В высоконапорных гидромашинах, например гидравлических прессах, может происходить ламинарное течение жидкости через малые зазоры при больших перепадах давлений порядка нескольких десятков и даже сотен мегапаскалей.

Опыт показывает, что в таких случаях падение напора вдоль потока оказывается существенно нелинейным, а закон Пуазейля дает заметную погрешность.

При таких течениях необходимо учитывать нагревание жидкости, которое ведёт к уменьшению её вязкости, причем степень влияния этого фактора будет нарастать вдоль потока жидкости. С другой стороны, с увеличением давления вязкость жидкостей возрастает. Таким образом, вязкость жидкости переменна вдоль потока и, как результат одновременного действия двух указанных факторов, продольный градиент давления

, обусловленный трением, оказывается непостоянным.

Указанные факторы действуют и на расход: повышение температуры способствует его увеличению, а высокое давление в жидкости - его уменьшению, по сравнению со значением, определяемым законом Пуазейля. Таким образом, влияние этих двух факторов на расход является противоположным.

Рассмотрим задачу о ламинарном течении в зазоре толщиной а, длиной l и шириной b с учетом влияния на вязкость давления и температуры. При этом допускаем, что плотность жидкости не зависит от давления и температуры, а размеры зазора таковы, что его толщина существенно меньше ширины.

Ранее было установлено, что расход через плоскую щель составляет

Физическая сущность первого сомножителя в этом произведении – потери на трение по длине щели. Он показывает, как быстро теряется энергия по ходу течения жидкости. Причём потери на трение

есть ни что иное, как уменьшение давления по длине щели l. Если учесть сказанное и перейти к пределу, эту величину можно характеризовать падением давления по длине зазора вида:

Знак « - » в этой формуле показывает, что давление по длине зазора уменьшается.

С учётом последнего и в пересчёте на единичную ширину зазора (b=1) расход через щель можно записать в виде

При рассмотрении свойств жидкости упоминались формулы, учитывающие изменение коэффициента динамической вязкости

от температуры:

и давления:

Для одновременного учёта влияния на вязкость жидкости давления и температуры можно принять

.

В приведённых формулах, напомним, использованы следующие обозначения:

?t – динамический коэффициент вязкости при заданной температуре,

?P – динамический коэффициент вязкости при заданном давлении,

T0, P0, ?0 – температура, давление и динамический коэффициент вязкости жидкости в начале зазора,

T, P, ? – температура, давление и динамический коэффициент вязкости жидкости в конце зазора,

kt – коэффициент, для минеральных масел равный 0,02-0,03,

kP – коэффициент, для минеральных масел равный 0,002-0,003,

e – основание натурального логарифма, равное 2,718282.

Теперь запишем уравнение тепловой энергии, т. е. равенство между потерей энергии на трение, превратившейся в тепло, и приростом тепловой энергии жидкости за единицу времени:

,

где С - теплоемкость жидкости,

k — коэффициент, учитывающий долю работы сил вязкости, которая идет на нагревание жидкости.

При k = 1 теплоотдача в стенку отсутствует, и вся теряемая энергия, обусловленная вязким трением, идет на нагревание жидкости. При k = 0 происходит максимальная теплоотдача в стенку, в результате чего повышения температуры жидкости не происходит (изотермическое течение).

Из последнего равенства можно получить:

После подстановки этого равенства в выражение степени формулы для

получим:

Произведём разделение переменных в уравнении расхода через зазор

Используем полученную связь между ? и P выполним подстановку:

Произведём алгебраические преобразования: домножим обе части на

и поменяем знак степени при e (

Проинтегрируем последнее выражение:

Результатом интегрирования, будет равенство:

Постоянную интегрирования С1 найдем, учитывая, что в начальном сечении потока при l= 0 P = Р0. Cледовательно:

Подставив постоянную интегрирования C1, получим

.

Выразим отсюда Q:

.

Приведённую формулу можно анализировать с различных позиций. Мы посмотрим на неё только с одной точки зрения. Сравним её с формулой расхода через щель, полученную на основании закона Пуазейля. Расход по закону Пуазейля линейно изменяется при изменении давления. Последняя же формула, учитывающая изменение вязкости при изменении давления и теплообмен в потоке, что имеет место, когда жидкость движется с большими скоростями и при больших перепадах давления, описывает связь давления и расхода степенной функцией. При этом чем выше давление, тем больше отклонение расхода от линейной зависимости, соответствующей закону Пуазейля. Объясняется это тем, что расход жидкости при ламинарном течении пропорционален перепаду давления ?P, а величина потерянной энергии, равная произведению ?PQ, пропорциональна квадрату перепада давления. По этой причине потеря энергии на единицу расхода жидкости растет пропорционально перепаду давления.

Течение с облитерацией

При течении жидкости через капилляры, а также малые зазоры наблюдается явление, которое нельзя объяснить законами гидравлики. Это явление заключается в том, что расход жидкости через капилляр или зазор с течением времени уменьшается, несмотря на то, что перепад давления, при котором происходит движение жидкости, и ее физические свойства остаются неизменными. Причина этого явления кроется в том, что при определенных условиях происходит как бы засорение (заращивание) канала твердыми частицами, причем в зазорах и капиллярных каналах размером, меньшим 0,01 мм, может произойти полное заращивание проходного сечения и уменьшение расхода до нуля. Этот процесс носит название облитерации и заключается в том, что на поверхности раздела твердого тела и жидкости происходит под действием молекулярных и электромагнитных сил, возникающих между стенкой и жидкостью, адсорбция, т.е. уплотнение жидкости до практически твердого состояния на поверхности стенки.

Степень облитерации зависит от молекулярной структуры жидкости, причем это явление в большей степени проявляется в сложных, высокомолекулярных жидкостях типа масляной смеси на керосиновой основе, применяемой в силовых гидросистемах. Толщина адсорбционного слоя для жидкостей этого типа составляет несколько микрометров. Поэтому при течении через капилляры и малые зазоры этот слой может существенно уменьшить площадь поперечного сечения канала или даже полностью его перекрыть.

С повышением температуры интенсивность адсорбции, а следовательно, и облитерации, понижается. Повышение перепада давления, под которым происходит движение жидкости через зазор или капилляр, наоборот, увеличивает степень облитерации.

Если одна из стенок, образующих зазор, приводится в движение, т.е. происходит сдвиг, то образованные адсорбционные слои разрушаются, облитерация устраняется и восстанавливается первоначальный расход жидкости через зазор. Однако для такого сдвига обычно требуется значительное усилие. В зазорах между подвижной и неподвижной стенками облитерации не происходит.

Для избегания облитерации каналов жиклеров и дросселей рекомендуется их отверстия выполнять не меньше 0,2—0,4 мм. Для устранения облитерации через дросселирующее отверстие пропускают стержень, перемещающийся возвратно-поступательно и обеспечивающий автоматическую прочистку отверстия (разрушение адсорбционного слоя).

Течение с теплообменом

В рассмотренных выше случаях ламинарного течения не учитывалось изменение температуры и, следовательно, изменение вязкости жидкости как в пределах поперечного сечения, так и вдоль потока, т.е. предполагалось постоянство температуры во всех точках потока. Подобное течение называют изотермическим. В общем случае, конечно, течение жидкости по гидросистеме сопровождается изменением температуры.

Очевидно, что если по трубопроводу движется жидкость, температура которой значительно выше температуры окружающей среды, то такое течение сопровождается теплоотдачей через стенку трубы во внешнюю среду и, следовательно, охлаждением жидкости. Когда же температура движущейся жидкости ниже температуры окружающей среды, то происходит приток тепла через стенку трубы. В результате жидкость в процессе течения нагревается.

В обоих указанных случаях при течении жидкости осуществляется теплообмен с внешней средой. При этом температура и вязкость жидкости, непостоянны, а течение не изотермическое.

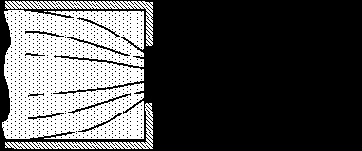
Поэтому зависимости, полученные в предположении постоянства вязкости по сечению потока, при течении со значительным теплообменом нуждаются в поправках. При течении жидкости, сопровождающемся её охлаждением, слои жидкости, непосредственно прилегающие к стенке, имеют температуру ниже, а вязкость выше, чем в основной части потока. Вследствие этого торможение в пристенных слоях жидкости более интенсивное, а градиент скорости у стенки меньше градиента скорости в основной части потока.

При течении же, сопровождающемся нагреванием жидкости, обусловленным притоком тепла через стенку, пристенные слои жидкости будут иметь более высокую температуру и меньшую вязкость, вследствие чего градиент скорости у стенки будет больше, чем в основной части потока. Таким образом, вследствие теплообмена через стенку трубы между жидкостью и внешней средой происходит нарушение параболического закона распределения скоростей по сечению потока.

На рисунке показаны сравнительные графики распределения скоростей при изотермическом течении (линия 1), при течении с охлаждением жидкости (линия 2) и при течении с её нагреванием (линия 3).
Из рисунка следует, что охлаждение жидкости влечет за собой увеличение неравномерности распределения скоростей, а нагревание – уменьшение, по сравнению с обычным параболическим распределением скоростей.

Изменение профиля скоростей при отклонении от изотермического течения вызывает изменение закона сопротивления потоку жидкости.

При ламинарном течении вязких жидкостей в трубах с теплообменом (охлаждением) сопротивление получается больше, а при течении с притоком тепла (нагреванием) меньше, чем при изотермическом течении.

Ввиду того, что точное решение задачи о течении жидкости с теплообменом представляет большую сложность, так как приходится учитывать переменность температуры и вязкости жидкости по поперечному сечению и вдоль трубы, а также рассматривать тепловые потоки в разных сечениях трубы, для практических расчетов пользуются следующей, приближенной формулой для определения коэффициента потерь на трение с учётом теплообмена

где Reср.ж - число Рейнольдса, подсчитанное по средней вязкости жидкости,

?ср.t ст - вязкость жидкости, соответствующая средней температуре стенки,

?ср - средняя вязкость жидкости.

Температурное расширение жидкости

Температурное расширение жидкости состоит в том, что она может изменять свой объем при изменении температуры. Это свойство характеризуется температурным коэффициентом объемного расширения, представляющим относительное изменение объема жидкости при изменении температуры на единицу (на 1оC) и при постоянном давлении:

По аналогии со свойством сжимаемости жидкости можно записать

или через плотность

Изменение объёма при изменении температуры происходит за счёт изменения плотности.

Для большинства жидкостей коэффициент bt с увеличением давления уменьшается. Коэффициент bt с уменьшением плотности нефтепродуктов от 920 до 700 кг/м3 увеличивается от 0,0006 до 0,0008; для рабочих жидкостей гидросистем bt обычно принимают не зависящим от температуры. Для этих жидкостей увеличение давления от атмосферного до 60 МПа приводит к росту bt примерно на 10 – 20 %. При этом, чем выше температура рабочей жидкости, тем больше увеличение bt. Для воды с увеличением давления при температуре до 50 оC bt растёт, а при температуре выше 50 оC уменьшается.

Типы потоков жидкости

Совокупность элементарных струек жидкости представляет собой поток жидкости. Различают следующие типы потоков (или типы движений жидкости).

Напорные потоки (напорные движения) - это такие, когда поток ограничен твердыми стенками со всех сторон, при этом в любой точке потока давление отличается от атмосферного обычно в большую сторону, но может быть и меньше атмосферного. Движение в этом случае происходит за счёт напора, создаваемого, например, насосом или водонапорной башней. Давление вдоль напорного потока обычно переменное. Такое движение имеет место во всех гидроприводах технологического оборудования, водопроводах, отопительных системах и т.п.

Безнапорные потоки (безнапорные движения) отличаются тем, что поток имеет свободную поверхность, находящуюся под атмосферным давлением. Безнапорное движение происходит под действием сил тяжести самого потока жидкости. Давление в таких потоках примерно одинаково и отличается от атмосферного только за счет глубины потока. Примером такого движения может быть течение воды в реке, канале, ручье.

Свободная струя не имеет твёрдых стенок. Движение происходит под действием сил инерции и веса жидкости. Давление в таком потоке практически равно атмосферному. Пример свободной струи – вытекание жидкости из шланга, крана и т.п.

Трубопроводы с насосной подачей жидкости

В большинстве гидравлических систем технологического оборудования в качестве источника энергии используются насосы различного принципа действия. Важнейшей задачей, которая возникает при проектировании каждой гидросистемы, является согласование работы насосной станции и системы трубопроводов, гидроаппаратов и гидромашин, входящих в её состав. Это многообразные и сложные задачи, которые подробно рассматриваются в курсах, связанных с изучением гидропривода. Здесь мы познакомимся лишь с общим принципом таких расчётов.

Для этого рассмотрим наиболее простой случай трубопровода, по которому насос перекачивает жидкость из гидробака в ёмкость или полость с заданными величинами давления и расхода. К таким ёмкостям можно отнести, например, гидроцилиндр. Нивелирными высотами, как и в предыдущих случаях, пренебрежём из-за их малости.

Запишем сначала уравнение Бернулли для сечений 2 и 3

где

- суммарные потери давления в напорном трубопроводе (характеристика напорного трубопровода).

Теперь запишем уравнение Бернулли для сечений 0 и 1

где

- атмосферное давление,

- суммарные потери давления во всасывающем трубопроводе (характеристика всасывающего трубопровода).

Из второго уравнения определим общий напор (энергию), которым обладает жидкость при входе в насос. Тогда второе уравнение примет вид

В процессе своей работы насос передаёт жидкости дополнительную энергию Hнасоса, в результате чего общий напор жидкости в сечении 2 становится равным:

т.е. можно записать:

Выделим из полученного равенства величину Hнасоса:

Перегруппируем члены в этом выражении:

Если принять, что:

§ в первом слагаемом атмосферное давление P0 равно 0,

§ второе слагаемое (скоростной напор на выходе из напорного трубопровода) можно переписать через расход и представить в виде

, где

можно считать коэффициентом скоростного напора (в этом выражении ? – площадь сечения трубопровода),

§ третье слагаемое можно представить в виде суммарной характеристики всасывающего и напорного трубопровода, то последнее выражение примет вид:

Последнее выражение представляет собой рабочую характеристику насоса.

Построив характеристику трубопровода

и характеристику насоса можно найти так называемую рабочую точку, как точку пересечения характеристик насоса и трубопровода. Это означает, что при соответствующих этой точке давлении и расходе, будет обеспечиваться работа насоса с требуемыми характеристиками. Чтобы получить другую рабочую точку нужно или изменить рабочую характеристику насоса или характеристику трубопровода. Это можно сделать различными способами, например, изменив сопротивление трубопровода или режим работы насоса.

Турбулентное течение в гладких трубах

Гладкие или точнее технически гладкие трубы это такие, шероховатость внутренних поверхностей которых настолько мала, что практически не влияет на потери энергии на трение. К таким трубам относят

цельнотянутые трубы из цветных металлов, трубы из алюминиевых сплавов, стальные высококачественные бесшовные трубы, новые высококачественные чугунные трубы, новые не оцинкованные трубы.

В основном трубы, используемые в гидросистемах технологического оборудования можно отнести к технически гладким.

Потери напора при турбулентном течении жидкости, как уже отмечалось ранее, могут быть определены по формуле Дарси

или в виде потерь давление на трение

Однако коэффициент потерь на трение по длине в этом случае будут значительно больше, чем при ламинарном движении.

Причём сам коэффициент

будет существенно зависеть от числа Рейнольдса. Эту зависимость можно представить в виде графика.

Наиболее применимыми формулами для определения

являются следующие эмпирические и полуэмпирические зависимости

применяемая для чисел Рейнольдса в пределах 2300

несколько миллионов, или

используемая в интервале 2300

100000.

Турбулентное течение в шероховатых трубах

Исследование течения жидкости в шероховатых трубах практически полностью основываются на экспериментальных исследованиях. На их результатах основаны зависимости и расчётные формулы, применяющиеся для определения потерь энергии в подобных условиях. Основная формула для определения потерь напора – формула Дарси. Отличие заключается только в коэффициенте потерь на трение. В отличие от турбулентных потоков в гладких трубах, где коэффициент на трение полностью определяется числом Рейнольдса Re, для потоков в трубах имеющих шероховатые внутренние поверхности

зависит ещё и от размеров этой шероховатости. Установлено, что решающее значение имеет не абсолютная высота неровностей (абсолютная шероховатость) k, а отношение высоты этих неровностей к радиусу трубы r0. Эта величина обозначается

и называется относительной шероховатостью. Одна и та же абсолютная шероховатость может практически не влиять на коэффициент трения в трубах большого диаметра, и существенно увеличивать сопротивление в трубах малого диаметра. Кроме того,

на сопротивление потоку жидкости влияет характер шероховатости. По характеру шероховатость разделяют на естественную, при которой величина неровностей k по длине трубы различна, и регулярную, при которой размеры неровностей по всей трубе одинаковы. Регулярная шероховатость создаётся

искусственно и характеризуется тем, что имеет одинаковую высоту и форму неровностей по всей длине трубы. Шероховатость такого вида называют равномерно распределённой зернистой шероховатостью. Коэффициент потерь на трение в этом случае описывается функцией

Экспериментальным изучением влияния числа Рейнольдса и относительной шероховатости занимался Никурадзе И. И., который проводил опыты для диапазонов

Результаты этих исследований сведены к графику в логарифмических координатах.

На графике цифрами обозначены:

1 – зона ламинарного течения, коэффициент

вычисляется по формуле

;

2 – зона турбулентного гладко стенного течения, коэффициент

вычисляется по формуле

Турбулентное течение в трубах

Несмотря на то, что в общем случае турбулентное движение жидкости является неустойчивым, если рассматривать некоторые усредненные по времени характеристики потока, среднюю скорость, среднее распределение скоростей по сечению, среднее давление, средние величины пульсаций, а также среднее значение расхода, то во многих случаях они могут оказаться постоянными. Именно такие характеристики мы и будем использовать при описании турбулентных потоков.

Многочисленными опытами установлено, что турбулентный поток, как правило, не соприкасается со стенками трубы, а занимает только центральную часть. Между стенками трубы и турбулентным потоком существует тонкий слой жидкости, течение в котором является ламинарным. Причём внешняя часть этого слоя, соприкасающаяся с поверхностью трубы, неподвижна (имеет нулевую скорость), а его внутренняя часть, непосредственно взаимодействующая с потоком, имеет скорость, соизмеримую со средней скоростью жидкости в данном сечении. Таким образом, турбулентный поток движется как бы в трубе из ламинарного слоя той же жидкости. Толщина этого слоя весьма мала. Её можно определить по формуле:

где d – внутренний диаметр трубы,

?Т – коэффициент потерь на трение при турбулентном режиме течения.

Можно считать, что скорость жидкости внутри этого слоя по толщине меняется по линейному закону. Надо так же отметить, что число Рейнольдса Reлс (число Рейнольдса для ламинарного слоя), подсчитанное по толщине слоя

, скорости внутренней части ламинарного слоя

и кинематическому коэффициенту вязкости

есть величина постоянная.

Эта величина имеет постоянное значение для любых турбулентных потоков. Поэтому при увеличении скорости потока растёт скорость ламинарного слоя, а его толщина уменьшается. При больших значениях Re (больших скоростях) ламинарный слой практически исчезает.

Ударное давление

Для выяснения величины подъёма давления

Р применим теорему о сохранении количества движения (импульса силы). Для этого рассмотрим элементарное перемещение участка жидкости длинной dL за время dt. Учтём, что при прямом гидроударе кинетическая энергия ударной волны полностью превращается в потенциальную, т.е. скорость жидкости V становится равной нулю 0.

Импульс силы, под действием которого происходит это движение, равен:

Изменение количества движения рассматриваемого объёма длиной dL будет:

Повторимся: скорость во второй скобке равна 0, т.к. рассматриваемый объём жидкости останавливается.

Приравнивая эти выражения по теореме о сохранении количества движения, получим:

Отсюда выразим величину повышения давления ?P:

После замены дроби скоростью a, окончательно будем иметь:

где V - скорость жидкости в трубопроводе до возникновения гидроудара,

- плотность жидкости,

а – скорость распространения ударной волны.

Если в эту формулу подставить выражение описывающее a, то придём к формуле, носящей имя Жуковского:

Удельный вес

Удельным весом жидкости

- называется вес единицы её объёма. Эта величина выражается формулой для бесконечно малого объёма жидкости dW с весом dG:

Для однородных жидкостей можно считать:

где G – вес жидкости.

Удельный вес жидкости и плотность связаны соотношением:

где g – ускорение свободного падения.

Единицы измерения: [Н/м3], [Н/дм3], [Н/л], [Н/см3], 1Н=1кг•м/с2.

Значение ускорения свободного падения g на земле изменяется от 9,831м/с2 на полюсах до 9,781 м/с2 на экваторе.

Уравнение Бернулли

Выше уравнение Бернулли для струйки идеальной жидкости получено строгими математическими методами, использующимися в классической гидромеханике. То же уравнение можно получить (нестрого), используя рассуждения, которые часто применяются в гидравлике.

Уравнение Бернулли для потока идеальной жидкости

Поток идеальной жидкости, как указывалось ранее, можно представить совокупностью элементарных струек жидкости. Скорости по сечению потока неодинаковы, причём в середине потока скорости наибольшие, а к периферии они уменьшаются (струйная модель потока). Это означает, что различные струйки в одном сечении имеют различные значения кинетической энергии. Отсюда следует, что кинетическая энергия, посчитанная с использованием скоростей элементарных струек u?, и кинетическая энергия, посчитанная с использованием значения средней скорости потока V, будет иметь разные значения. Выясним, какова эта разница. Кинетическая энергия элементарной струйки

равна:

где

- масса жидкости плотностью

, протекающей через живое сечение элементарной струйки

со скоростью

за время dt, равная:

Проинтегрировав выражение для

, получим выражение для кинетической энергии потока идеальной жидкости

Если принять, что t=1, получим:

Последняя формула определяет энергию потока с использованием скоростей элементарных струек u?.

Если получить значение кинетической энергии потока с использованием значения средней скорости потока V , получим формулу:

где

- масса жидкости плотностью

, протекающей через живое сечение потока

со скоростью

за время t, равная:

После подстановки при t=1 окончательно получим:

Отношение

, равное:

Полученная величина ? носит наименование коэффициент а кинетической энергии или коэффициента Кориолиса. Смысл этого коэффициента заключается в отношении действительной кинетической энергии потока в определённом сечении к кинетической энергии в том же сечении потока, но при равномерном распределении скоростей. При равномерном распределении скоростей его значение равно единице, а при неравномерном – всегда больше единицы и для любого потока его значение находится в пределах от 1 до 2 и более.

Учитывая коэффициент кинетической энергии, приведём уравнение Бернулли для потока идеальной жидкости, которое примет вид:

Надо учесть, что в общем случае в разных сечениях потока коэффициент ? будет иметь различные значения.

Уравнение Бернулли для потока реальной жидкости

В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т.е. напор потока Hпотока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2, то потери гидродинамического напора ?h составят:

где H1-1- напор в первом сечении потока жидкости,

H2-2 - напор во втором сечении потока,

?h - потерянный напор - энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения 2-2.

С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть

Индексами 1 и 2 обозначены характеристики потока в сечениях 1-1 и 2-2.

Если учесть, что характеристики потока V и ? зависят от геометрии потока, которая для напорных потоков определяется геометрией трубопровода, понятно, что потери энергии (напора) в разных трубопроводах будут изменяться неодинаково. Показателем изменения напора потока является гидравлический уклон I, который характеризует потери напора на единице длины потока. Физический смысл гидравлического уклона – интенсивность рассеяния энергии по длине потока. Другими словами, величина I показывает, как быстро трубопровод поглощает энергию потока, протекающего в нём

Изменение энергии по длине потока удобно проследить на графиках. Из уравнения Бернулли для потока реальной жидкости (закона сохранения энергии) видно, что гидродинамическая линия для потока реальной жидкости (с одним источником энергии) всегда ниспадающая. То же справедливо и для пьезометрической линии, но только в случае равномерного движения, когда скоростной напор

а уменьшение напора происходит только за счёт изменения потенциальной энергии потока, главным образом за счёт уменьшения давления P.

Уравнение Бернулли для струйки идеальной жидкости

Рассмотрим элементарную струйку идеальной жидкости при установившемся движении, в которой выделим два сечения 1-1 и 2-2. Площади живых сечений потока обозначим d?1 и d?2. Положение центров тяжести этих сечений относительно произвольно расположенной линии сравнения (нулевой линии) 0 - 0 характеризуется величинами z1 и z2. Давления и скорости жидкости в этих сечениях имеют значения P1, P2 и u1, u2 соответственно.

Будем считать, что движение струйки жидкости происходит только под действием силы давления (внутреннее трение в жидкости отсутствует), а давление обладает свойствами статического и действует по нормали внутрь рассматриваемого объёма.

За малый промежуток времени dt частицы жидкости из 1-1 переместятся в 1'-1' на расстояние, равное u1dt, а частицы из 2-2 в 2' - 2' на расстояние u2dt.

Согласно теореме кинетической энергии приращение энергии тела (в данном случае выделенного объёма жидкости) равно сумме работ всех действующих на него сил.

Работу в данном случае производят силы давления, действующие в рассматриваемых живых сечениях струйки 1-1 и 2-2, а также силы тяжести. Тогда работа сил давления в сечении 1-1 будет положительна, т.к. направление силы совпадает с направлением скорости струйки. Она будет равна произведению силы p1d?1 на путь u1dt:

Работа сил давления в сечении 2-2 будет отрицательной, т.к. направление силы противоположно направлению скорости. Её значение

Полная работа, выполненная силами давления, примет вид:

Работа сил тяжести равна изменению потенциальной энергии положения выделенного объёма жидкости при перемещении из сечения 1-1 в сечение 2-2. С учётом условия неразрывности потока и несжимаемости жидкости выделенные элементарные объёмы будут равны и, следовательно, будут равны их веса dG:

При перетекании от сечения 1-1 в сечение 2-2 центр тяжести выделенного объёма переместится на разность высот (z1 – z2) и работа, произведённая силами тяжести, составит:

Проанализируем теперь изменение кинетической энергии рассматриваемого объёма элементарной струйки жидкости.

Приращение кинетической энергии выделенного объёма за dt равно разности его кинетических энергий в сечениях 1-1 и 2-2. Это приращение составит

.

Приравнивая приращение кинетической энергии сумме работ сил тяжести и сил давления, придём к виду:

.

Разделив обе части на вес dG, т.е. приведя уравнение к единичному весу, получим

.

После сокращения и преобразований придём к искомому виду

Если учесть, что сечения 1-1 и 2-2 выбраны произвольно, можно прийти к выводу, что сумма приведённых выше величин

описывающих движение жидкости под действием сил давления и сил тяжести есть величина постоянная для элементарной струйки, т.е.

Таким образом, снова получено то же (ранее полученное интегрированием уравнений Эйлера) уравнение Бернулли для элементарной струйки невязкой жидкости при установившемся движении под действием сил тяжести.

Уравнение неразрывности для элементарной струйки жидкости

В технологическом оборудовании чаще всего рассматривают потоки, в которых не образуются разрывы жидкости, т.е. жидкость сплошь заполняет пространство.

Рассмотрим элементарную струйку несжимаемой жидкости при установившемся движении, в которой выделим два произвольных сечения 1-1 и 2-2, расположенные на некотором расстоянии одно от другого. Здесь d?1 и d?2 – площади, u1 и u2 – скорости, dQ1 и dQ2 – расходы элементарной струйки в соответствующих живых сечениях.

Очевидно, что

причём dQ1 втекает в рассматриваемый участок элементарной струйки, а dQ2 – вытекает.

Учтём, что форма элементарной струйки не изменяется с течением времени, а поперечный приток и отток невозможны, так как скорости на боковой поверхности струйки направлены по касательным к линиям тока, из которых состоит эта боковая поверхность, тогда получаем, что расходы dQ1 и dQ2 равны, т.е.

Вследствие того, что сечения 1-1 и 2-2 выбраны произвольно, подобные соотношения справедливы для любых сечений элементарной струйки. Следовательно, можно записать:

или

Последнее соотношение называется уравнением неразрывности в гидравлической форме для элементарной струйки несжимаемой жидкости при установившемся движении.

Уравнение неразрывности в гидравлической форме для потока жидкости при установившемся движении

Если просуммировать расходы всех элементарных струек в каждом живом сечении потока, то получится уравнение неразрывности для потока при установившемся движении. Обычно его записывают в следующих видах:

или

Из сказанного видно, что для несжимаемой жидкости при установившемся движении жидкости расход во всех живых сечения потока одинаков, несмотря на то, что площади живого сечения и средние скорости в каждом сечении и могут быть разными.

Из уравнения неразрывности вытекает следующее важное соотношение:

т.е. средние скорости в живых сечениях потока обратно пропорциональны их площадям.

Уравнение неразрывности потока жидкости в гидравлической форме очень часто применяется в гидравлике для описания движения жидкости в каналах и трубопроводах.

Виды движения (течения) жидкости

Течение жидкости вообще может быть неустановившимся (нестационарным) или установившимся (стационарным).

Неустановившееся движение – такое, при котором в любой точке потока скорость движения и давление с течением времени изменяются, т.е. u и P зависят не только от координат точки в потоке, но и от момента времени, в который определяются характеристики движения т.е.:

Примером неустановившегося движения может являться вытекание жидкости из опорожняющегося сосуда, при котором уровень жидкости в сосуде постепенно меняется (уменьшается) по мере вытекания жидкости.

Установившееся движение – такое, при котором в любой точке потока скорость движения и давление с течением времени не изменяются, т.е. u и P зависят только от координат точки в потоке, но не зависят от момента времени, в который определяются характеристики движения:

и, следовательно,

Пример установившегося движения - вытекание жидкости из сосуда с постоянным уровнем, который не меняется (остаётся постоянным) по мере вытекания жидкости.

В случае установившегося течения в процессе движения любая частица, попадая в заданное, относительно твёрдых стенок, место потока, всегда имеет одинаковые параметры движения. Следовательно, каждая частица движется по определённой траектории.

Траекторией называется путь, проходимый данной частицей жидкости в пространстве за определенный промежуток времени.

При установившемся движении форма траекторий не изменяется во время движения. В случае неустановившегося движения величины направления и скорости движения любой частицы жидкости непрерывно изменяются, следовательно, и траектории движения частиц в этом случае также постоянно изменяются во времени.

Поэтому для рассмотрения картины движения, образующейся в каждый момент времени, применяется понятие линии тока.

Линия тока - это кривая, проведенная в движущейся жидкости в данный момент времени так, что в каждой точке векторы скорости ui совпадают с касательными к этой кривой.

Нужно различать траекторию и линию тока.
Траектория характеризует путь, проходимый одной определенной частицей, а линия тока направление движения в данный момент времени каждой частицы жидкости, лежащей на ней.

При установившемся движении линии тока совпадают с траекториями частиц жидкости. При неустановившемся движении они не совпадают, и каждая частица жидкости лишь один момент времени находится на линии тока, которая сама существует лишь в это мгновение. В следующий момент возникают другие линии тока, на которых будут располагаться другие частицы. Еще через мгновение картина опять меняется.

Если выделить в движущейся жидкости элементарный замкнутый контур площадью d? и через все точки этого контура провести линии тока, то получится трубчатая поверхность, которую называют трубкой тока. Часть потока, ограниченная поверхностью трубки тока, называется элементарной струйкой жидкости. Таким образом, элементарная струйка жидкости заполняет трубку тока и ограничена линиями тока, проходящими через точки выделенного контура с площадью d?. Если d? устремить к 0, то элементарная струйка превратится в линию тока.

Из приведённых выше определений вытекает, что в любом месте поверхности каждой элементарной струйки (трубки тока) в любой момент времени вектора скоростей направлены по касательной (и, следовательно, нормальные составляющие отсутствуют). Это означает, что ни одна частица жидкости не может проникнуть внутрь струйки или выйти наружу.

При установившемся движении элементарные струйки жидкости обладают рядом свойств:

площадь поперечного сечения струйки и ее форма с течением времени не изменяются, так как не изменяются линии тока; проникновение частиц жидкости через боковую поверхность элементарной струйки не происходит; во всех точках поперечного сечения элементарной струйки скорости движения одинаковы вследствие малой площади поперечного сечения; форма, площадь поперечного сечения элементарной струйки и скорости в различных поперечных сечениях струйки могут изменяться. Трубка тока является как бы непроницаемой для частиц жидкости, а элементарная струйка представляет собой элементарный поток жидкости.

При неустановившемся движении форма и местоположение элементарных струек непрерывно изменяются.

Кроме того, установившееся движение подразделяется на равномерное и неравномерное.

Равномерное движение характеризуется тем, что скорости, форма и площадь сечения потока не изменяются по длине потока.

Неравномерное движение отличается изменением скоростей, глубин, площадей сечений потока по длине потока.

Среди неравномерно движущихся потоков следует отметить плавно изменяющиеся движения, характеризующееся тем, что:

линии тока искривляются мало; линии тока почти параллельны, и живое сечение можно считать плоским; давления в живом сечении потока зависят от глубины.

Вязкое трение при турбулентном движении

Выделим в турбулентном потоке, движущимся параллельно твёрдой стенке, элементарную площадку ?S и определим касательное напряжение ?, возникающее за счёт пульсаций скоростей

. Через площадку в перпендикулярном потоку направлении, проходит расход жидкости

Масса жидкости, проходящая через площадку за время ?t, равна

За счёт составляющей пульсаций скорости

эта масса получит приращение количества движения

Приращение количества движения равно импульсу силы, т.е.

;

где сила

и тогда касательное напряжение будет равно

а его осреднённое по времени значение можно представить в виде

Определённое таким образом касательное напряжение вычислить очень трудно из-за неизвестных значений

, поэтому, чаще всего рассматривается приближённое решение.

Представим, что малый объём жидкости, находящийся в точке A и имеющий скорость

, в результате турбулентного перемешивания переместился в точку B, расположенную на расстоянии l от точки A приобрёл скорость

Будем считать, что пульсации скоростей

пропорциональны приращению скорости рассматриваемого объёма жидкости, т.е.

Тогда

можно представить в виде

где коэффициент пропорциональности включён в величину l, знак

совпадает со знаком производной

. Величина l носит называние путь перемешивания.

Последнее уравнение обычно преобразовывают к виду

где СТ – коэффициент перемешивания, или коэффициент турбулентного обмена который равен

Полученное уравнение аналогично уравнению касательного напряжения при ламинарном режиме. Коэффициент CТ значительно превышает по величине динамическую вязкость

и зависит от числа Рейнольдса.

Вязкость

Вязкость – свойство жидкости оказывать сопротивление относительному сдвигу ее слоев. Вязкость проявляется в том, что при относительном перемещении слоев жидкости на поверхностях их соприкосновения возникают силы сопротивления сдвигу, называемые силами внутреннего трения, или силами вязкости. Если рассмотреть то, как распределяются скорости различных слоёв жидкости по сечению потока, то можно легко заметить, что чем дальше от стенок потока, тем скорость движения частиц больше. У стенок потока скорость движения жидкости равна нулю. Иллюстрацией этого является рисунок, так называемой, струйной модели потока. На рисунке применены следующие обозначения:

- скорость слоя жидкости,

- расстояние между соседними слоями жидкости.

Медленно движущийся слой жидкости «тормозит» соседний слой жидкости, движущийся быстрее, и наоборот, слой, движущийся с большей скоростью, увлекает (тянет) за собой слой, движущийся с меньшей скоростью. Силы внутреннего трения появляются вследствие наличия межмолекулярных связей между движущимися слоями.

Внезапное расширение. Теорема Борда - Карно

В этом случае, одном из немногих, выражение для потери напора можно найти теоретическим путем.

При внезапном расширении потока в трубке от сечения 1 до сечения 2 жидкость не течёт по всему контуру стенок, а движется по плавным линиям токов. Вблизи стенок, где внезапно увеличивается диаметр трубы, образуется пространство, в котором жидкость находится в интенсивном вращательном движении. При таком интенсивном перемешивании происходит очень активное трение жидкости о твёрдые стенки трубы об основное русла потока, а также трение внутри вращающихся потоков, вследствие чего происходят существенные потери энергии. Кроме того, какая-то часть энергии жидкости затрачивается на фазовый переход частиц жидкости из основного потока во вращательные и наоборот. На рисунке видно, что показания пьезометра во втором сечении больше, чем в первом. Тогда появляется вопрос, о каких потерях идёт речь? Дело в том, что показания пьезометра зависят не только от потерь энергии, но и от величины давления. А давление во втором сечении становится больше из-за уменьшения скоростного напора за счёт расширения потока и падения скорости. В этом случае надо учитывать, что если бы не было потерь напора на местном сопротивлении, то высота жидкости во втором пьезометре была бы ещё больше.

Происходящая при внезапном расширении потеря напора может быть найдена с помощью уравнения Бернулли для потока реальной жидкости, записанного для сечений 1 и 2, где движение основного потока занимает всё сечение трубы, которое будет иметь вид:

Применим теорему механики об изменении количества движения к выделенному цилиндрическому объёму, заключённому между сечениями 1 и 2, равному импульсу внешних сил, действующих на рассматриваемый объём в направлении его движения. Этими силами будут силы от давления

в соответствующих сечениях, действующие на равные по размеру торцовые площади

. (Изменением давления по высоте потока в трубе и силами трения из-за малости участка пренебрежём.) Разность этих сил составляет величину

.

Этому импульсу соответствует секундное изменение количества движения жидкости, втекающей в рассматриваемый объём и вытекающей из него. Если считать, что скорости по сечениям распределены равномерно, получим:

.

Приравняем импульс сил и изменение количества движения по теореме об изменении количества движения

.

Разделим уравнение на

и учтём, что

Далее произведём сокращения, заменив величину

суммой

. Искусственно добавим в правую часть и тут же вычтем величину

.

Перегруппируем члены в правой части равенства

.

Заметим, что величина в скобках может быть упрощена

.

Проведя замену, получим

.

После перегруппировки членов получим

Разделим все члены равенства на

.

Окончательно уравнение примет вид

.

Сравним полученное уравнение с исходным уравнением для

, полученным из уравнения Бернулли:

.

Если допустить, что форма эпюр скоростей в первом и втором сечении одинакова, т.е.

и их значения приближаются к единице т.к. поток турбулентный, и поменять местами

, т.к.

, то из сравнения последних уравнений можно получить, что:

Назвав разность

потерянной скоростью, можно сказать, что потеря напора при внезапном расширении равна скоростному напору, подсчитанному по потерянной скорости. Это утверждение носит имя теоремы Борда - Карно.

Последнюю формулу можно переписать в виде:

или

.

С учетом того, что на основании уравнения неразрывности потока

, те же потери напора можно представить в виде:

или

.

Сравнивая последние выражения с формулой Вейсбаха

, можно выделить выражения для коэффициента местного сопротивления при внезапном расширении потока:

, если

определять по скорости

;

, если

определять по скорости

Внезапное сужение потока

При внезапном сужении, так же как и при внезапном расширении потока, создаются пространства с завихрениями вращающейся жидкости, которые образуются в пристенном пространстве широкой части трубы. Такие же завихрения образуются в начале узкой части трубы за счёт того, что при входе в неё (узкую часть) жидкость продолжает некоторое время двигаться по инерции в направлении центра трубы, и основное русло потока ещё некоторое время продолжает сужаться. Следовательно, при внезапном сужении потока возникает как - бы два подряд идущих местных сопротивления. Местное сопротивление за счёт сужения основного русла и сразу же за ним местное расширение, уже рассмотренное выше. С учётом этого потери напора при внезапном сужении примут вид

;

где

- коэффициент местного сопротивления за счёт сужения потока,

- средняя скорость потока в самом узком месте основного русла (в сечении у),

- средняя скорость потока в сечении 2.

Для практических расчётов чаще всего пользуются следующей полуэмпирической формулой:

где

- степень сужения трубы.

Внезапный поворот потока

Такое местное сопротивление, называемое обычно коленом, очень сильно влияет на потери напора. В нём происходит отрыв потока от стенки трубы и создаются две сложные вихревые зоны, в которых интенсивно теряется энергия. Степень интенсивности существенно зависит от угла поворота

. Коэффициент местного сопротивления значительно возрастает с увеличением угла поворота, и его можно определить по эмпирической формуле

В гидросистемах подобных местных сопротивлений рекомендуется избегать.

Возникновение ламинарного режима

В реальных гидросистемах, даже при ламинарном режиме течения жидкости в круглых трубах, на пути потока встречаются участки с другой геометрией. Это могут быть соединения труб, изгибы, гидроаппараты и т.п. На таких участках характер потока меняется, режим движения становится турбулентным.

Однако после прохождения такого участка при входе жидкости в прямую трубу при соответствующей скорости устанавливается параболическое распределение скоростей. Поток снова стремится к ламинарному режиму движения. Происходит это не моментально, а в течение некоторого времени на отрезке трубы определённой длины. Такой отрезок называют начальным участком ламинарного течения lнач.

Длину такого участка можно определить из формулы Шиллера

где d – диаметр трубы.

Отсюда, если в качестве Re взять критическое число Рейнольдса легко получить, что максимально возможная длина такого участка равна

Потери энергии на этом участке будут несколько больше, чем в остальной части трубы. С учётом этого формула для расчёта потерь напора на трение hтр при ламинарном движении в круглых гладких трубах принимает вид

Для коротких труб такое уточнение потерь напора может иметь существенное значение, для длинных величину 0,165 можно не учитывать.

Возникновение турбулентного течения жидкости

Если на каком-то участке трубопровода существует турбулентный поток, то это не значит, что такой же характер сохраняется во всей трубе. На различных участках трубопровода и даже на одних и тех же участках в разные периоды времени поток может иметь различный характер. Это может определяться либо различными диаметрами трубопроводов, либо изменением скорости течения жидкости. Во всех случаях при возникновении условий турбулентного режима он устанавливается в трубе не мгновенно. Это происходит в течение некоторого времени на участке трубы определённой длины. Рассмотрим процесс возникновения турбулентного режима движения.

Переход к турбулентному режиму может происходить из ламинарного, например, в результате плавного или внезапного изменения диаметра трубы Такой же переход возможен за счёт изменения скорости движения жидкости. К образованию турбулентного режима может приводить также и изменение формы потока жидкости.

Кроме перечисленных возможны и другие причины, особенно при режимах, характеризующихся числами Рейнольдса, близкими к критическому.

На основании опыта установлено следующее. Когда создаются условия для такого перехода, например, сужение проходного сечения трубы достигает значения, при котором поток может стать турбулентным, по периферии потока ламинарный слой нарушается и дальше по течению развивается турбулентный пограничный слой. Толщина этого слоя из-за турбулентного перемешивания достаточно быстро увеличивается, и турбулентный поток заполняет всё сечение трубопровода. Участок, на котором происходит превращение ламинарного режима движения в турбулентный, называется разгонным участком. Его длина

по экспериментальным данным равна

где d – диаметр трубопровода.

Выводы из графиков Никурадзе

Ø При ламинарном течении шероховатость практически не влияет на сопротивление. Эксперимент практически полностью подтверждает с теоретические формулы.

Ø Критическое число Рейнольдса от шероховатости не зависит (штриховые кривые отклоняются от прямой A в одной точке).

Ø В области турбулентных течений при небольших числах Рейнольдса и малой шероховатости сопротивление от шероховатости не зависит (штриховая линия совпадает с прямой B), а с увеличением Re сопротивление возрастает.

Ø При больших значениях чисел Рейнольдса

перестаёт зависеть от Re и становится постоянным для определённой относительной шероховатости.

Зачем гидравлика в машиностроении?

Важнейшей частью почти любого технологического оборудования, станка, пресса, робота и т.д. является привод. Простейшим образом привод можно понимать как совокупность устройств, предназначенных для преобразования и передачи энергии, необходимой для осуществления технологического движения с заданными кинематическими и силовыми характеристиками. В технике широко применяются механический, электрический, пневматический (газовый, чаще всего воздушный) и гидравлический приводы и их комбинации. Важнейшей характеристикой любого привода является крутящий момент (или сила), который он может обеспечивать при одних и тех же размерах или весе. Попытаемся сравнить по этому показателю электрический, пневматический и гидравлический приводы.

Для подобного анализа приводов рассмотрим основной, наиболее часто встречающийся элемент привода – двигатель вращения. Любой такой двигатель принципиально состоит из неподвижного статора и вращающегося внутри него ротора. При этом в любом двигателе можно считать, что ротор отталкивается от статора, в результате чего создаётся вращение.

Таким образом, можно считать, что между статором и ротором есть какая-то рабочая среда (рабочее тело), которая, упираясь в статор, толкает ротор. В электродвигателе это электромагнитное поле, в пневматическом двигателе это воздух, в гидродвигателе это жидкость. Чем больше сила отталкивания, тем больший крутящий момент развивает двигатель. Величина силы отталкивания зависит от того, как сильно сжата рабочая среда, т.е. от того, каковы внутренние напряжения рабочей среды.

Для любого двигателя (с некоторыми, непринципиальными допущениями) можно считать, что крутящий момент описывается функцией вида

где L – длина отталкивания ротора от статора,

r – радиус ротора,

? – радиальный зазор между ротором и статором,

P – напряжённость рабочей среды,

Z – количество пар элементов, взаимодействующих в процессе отталкивания ротора от статора (пары полюсов, пластины гидро- или пневмодвигателя и т.п.).

Опираясь на эту функцию, легко определить предельно возможные максимальные напряжения для любого двигателя как отношение развиваемого им крутящего момента к его геометрическим размерам.
Это формула будет иметь вид:

.

Величина P будет выражаться в единицах напряженности рабочей среды Н/м2.

Если таким способом проанализировать двигатели всех трёх типов, разделив их максимальные крутящие моменты на соответствующие геометрические характеристики, то можно установить следующее:

ü     P электромагнитного поля   -     около 1 МПа

ü     P газовой среды                     -      около 1 МПа

ü     P жидкостной среды               -     6,3-40 МПа и выше.

Следовательно, гидравлический привод во многие разы и даже десятки раз более энергоёмкий, чем электрический и пневматический.

При этом гидравлический привод имеет еще одну, очень важную особенность, которую можно проиллюстрировать на следующем опыте. Возьмём три одинаковых цилиндра. В первый цилиндр поместим два магнита одноимёнными полюсами навстречу друг к другу так, чтобы верхний магнит мог играть роль подвижного поршня. Во втором, заполненном воздухом, и третьем, заполненном жидкостью, установим плотно пригнанные поршни. Ко всем трём поршням приложим силы, сжимающие рабочие среды: электромагнитное поле, воздух и жидкость. При увеличении сил поршни начнут опускаться, а напряжение рабочих сред P будет расти. В цилиндре с жидкостью перемещение будет практически незаметным по сравнению с остальными цилиндрами. Т.е. жидкость по сравнению с газом и электромагнитным полем, практически несжимаема в большом диапазоне сил. Последнее проиллюстрировано на графике. Это качество обеспечивает высокую жёсткость гидропривода в большом диапазоне нагрузок.

Описанные особенности гидравлического привода определяют область его использования в технике. В большинстве случаев его применение обусловлено необходимостью в высоких энергетических показателях при малом весе или габаритах.

Загрязнение в процессе изготовления, сборки и испытания

Большое количество частиц загрязнения остаётся в гидросистеме и её элементах после изготовления и ремонта. Это песок, попадающий при литье; пыль, осевшая на стенках; окалина от сварки, ковки или термической обработки; остатки механической обработки деталей; заусенцы от трубопроводов; волокна ветоши, остающиеся после протирки. Притирочные пасты, применяемые при доводке гидроагрегатов, образуют смешанные с парафином, стеарином, воском и др. абразивные зёрна (карбиды бора и кремния, белый электрокорунд, алмазная пыль), твёрдость которых превышает твёрдость большинства конструкционных материалов. Паста при обработке деталей обычно накапливается в глухих ответвлениях системы и при её работе постепенно вымывается, циркулируя вместе с рабочей жидкостью.

Загрязнение в процессе эксплуатации

Наибольшее количество частиц загрязнения попадает в рабочие жидкости в процессе эксплуатации гидросистемы. За счёт износа её элементов рабочие жидкости загрязняются непрерывно самыми различными видами загрязнителей – ржавчиной, резиной, металлом, абразивными частицами, волокнистыми частицами, краской, пылью. Особенно интенсивный износ наблюдается в парах трения, дроссельных элементах, рабочих камерах гидромашин, распределительных устройствах плунжерных насосов и т.д. Продукты износа трущихся деталей поступают в жидкость непрерывно. При микроанализе проб жидкости было установлено, что размер металлических продуктов износа, генерируемых в рабочую жидкость, составляет от 1 до 10 мкм.

Совместное воздействие влаги, кислорода воздуха и рабочей жидкости может вызвать на поверхности деталей, трубопроводов, баков образование ржавчины и шелушение покрытий. Частицы ржавчины выпадают в виде осадка частиц микронных размеров. Этому способствует вибрация конструкции и пульсации давления.

Кроме того, загрязнения в жидкость попадают при обслуживании системы, при небрежном монтаже агрегатов, шлангов и трубопроводов, через незаглушенные соединительные узлы, из-за загрязнённости инструментов, заправочных средств, одежды обслуживающего персонала.

Источником загрязнения топлив и масел в некоторых случаях могут служить также сами фильтры, предназначенные для очистки жидкости. В процессе работы фильтрующие элементы частично разрушаются и их компоненты вымываются потоком жидкости. Такого типа загрязнения наблюдаются у всех фильтров с волокнистыми наполнителями, изготовленными, например, из бумаги, шерсти, войлока, целлюлозы, стекловолокна и т.п. Кроме того, при использовании волокнистых наполнителей, которые могут изменять пористость при увеличении перепада давлений во время гидроударов и пульсаций давления, задержанные фильтром частицы загрязнения медленно проходят через фильтроэлемент и вновь попадают в рабочую жидкость.

Загрязнение во время поставки, хранения и заправки

Различные присадки и добавки, предназначенных для улучшения эксплуатационных свойств жидкости в процессе транспортировки и хранения могут выделяться из жидкости, превращаясь в загрязняющие вещества. При длительном хранении в условиях положительных температур в маслах могут развиваться колонии микроорганизмов, водорослей и грибков. Размер отдельных грибков и бактерий, а также их спор составляет, как правило, 1 – 2 мкм, однако может достигать и 10 мкм. В основном их наблюдают на границе масло – вода. Непрерывно идёт процесс окисления масла. Активность этого процесса повышается с увеличением температуры и при наличии в масле эмульгированного воздуха. Катализатором окисления являются частицы износа из чёрных и цветных металлов. При окислении в масле образуются растворимые и нерастворимые продукты, которые способствуют его сгущению и могут, в конечном счёте, выпадать в виде осадка на детали гидроаппаратов и гидромашин. Мельчайшие нерастворимые продукты окисления коагулируют и укрупняются. Замечены случаи «самопроизвольного» увеличения размеров частиц загрязнений в герметически закрытых сосудах. Например, если при заправке в жидкости были зафиксированы частицы не более 10 мкм, то со временем обнаруживались частицы размером 25 – 200 мкм в виде рыхлых образований. Быстрый рост размера частиц происходит в жидкости, подвергающейся тряске при транспортировке. Жидкость может загрязняться частицами пыли из воздуха. Пыль поступает в баки через систему наддува и дренажа, через заливные горловины при «открытой» заправке баков. Пыль всегда присутствует в атмосфере. В одном литре воздуха число пылинок может изменяться от 10 до 200000. Предельная крупность частиц пыли в воздухе составляет 50 мкм, основную массу пыли составляют пылинки размером менее 10 мкм. В их составе:

до 80% - кварц твёрдостью 7 единиц по десятибалльной шкале (Мооса), до 17% - окись алюминия с твёрдостью 9 единиц, полевой шпат с твёрдостью 6 - 6,5 единиц, другие компоненты.

Для сравнения: твёрдость алмаза по десятичной шкале – 10, железа – 4,4, меди – 3,0, алюминия – 2,9.

Таким образом, большая доля частиц пыли соизмерима с зазорами в подвижных узлах гидроагрегатов, а твёрдость некоторых компонентов загрязнений значительно превосходит твёрдость материалов сопрягаемых деталей.

Заключение о подобии напорных потоков

Итак, в подобных напорных потоках имеем равенство безразмерных коэффициентов и чисел ?, ?, ?, Eu, Re, Ne. Изменение Re означает, что меняется соотношение основных сил в потоке, в связи с чем указанные коэффициенты могут также несколько меняться. Поэтому все эти коэффициенты следует рассматривать как функции Re (хотя в некоторых интервалах Re они могут оставаться постоянными).

Закон жидкостного трения – закон Ньютона

Если в равномерно движущемся потоке жидкости рассмотреть два соседних слоя с ординатами y1 и y2, расположенных на расстоянии dy друг от друга, и скорость первого из них обозначить u1, а скорость другого u2 , то разница между ними составит du. Тогда можно записать

Эта величина называется градиентом скорости по сечению потока или поперечным градиентом скорости. Он показывает, как меняются скорости слоёв жидкости по сечению потока.

Если между соседними слоями жидкости выделить некоторую площадку S, то согласно гипотезе Ньютона

где T – силы вязкого трения;

S – площадь трения;

? – коэффициент вязкого трения.

Величина ? в этом выражении является динамическим коэффициентом вязкости, равным

или

;

где ? – касательное напряжение в жидкости (зависит от рода жидкости).

Физический смысл коэффициента вязкого трения - число, равное силе трения, развивающейся на единичной поверхности при единичном градиенте скорости.

Единицы измерения: [Н·с/м2], [кГс·с/м2], [Пз]{Пуазейль}, 1Пз=0,1Н·с/м2.

На практике чаще используется кинематический коэффициент вязкости, названный так потому, что в его размерности отсутствует обозначение силы. Этот коэффициент представляет собой отношение динамического коэффициента вязкости жидкости к её плотности

Единицы измерения: [м2/c], [cм2/c], [Ст] {стокс}, [сСт] {сантистокс}, 1Ст=100сСт {1Ст=1 cм2/c}.

Жидкость как объект изучения гидравлики

Передачу энергии в гидравлических системах обеспечивают рабочие жидкости, поэтому чтобы эффективно их применять, надо знать какими свойствами они обладают.

Жидкости, как и все вещества, имеют молекулярное строение. Они занимают промежуточное положение между газами и твердыми телами. Это определяется величинами межмолекулярных сил и характером движений составляющих их молекул.

В газах расстояния между молекулами больше, а силы межмолекулярного взаимодействия меньше, чем в жидкостях и твердых телах, поэтому газы отличаются от жидкостей и твердых тел большей сжимаемостью. По сравнению с газами жидкости и твердые тела малосжимаемы.

Молекулы жидкости находятся в непрерывном хаотическом тепловом движении, отличающемся от хаотического теплового движения газов и твердых тел. В жидкостях это движение осуществляется в виде колебаний (1013 колебаний в секунду) относительно мгновенных центров и скачкообразных переходов от одного центра к другому. Тепловое движение молекул твердых тел состоит в колебаниях относительно стабильных центров. Тепловое движение молекул газа выглядит, как непрерывные скачкообразные перемены мест.

При этом надо заметить, что изменение температуры и давления приводят к изменениям свойств жидкостей. Установлено, что при повышении температуры и уменьшении давления свойства жидкостей приближаются к свойствам газов, а при понижении температуры и увеличении давления – к свойствам твердых тел.

Термин «жидкость» применяется для обозначения и собственно жидкости, которую рассматривают как несжимаемую или мало сжимаемую среду, и газа, который можно рассматривать как «сжимаемую жидкость».